
| A. | (-$\frac{π}{2}$,-$\frac{3π}{2}$) | B. | ($\frac{π}{2}$,$\frac{3π}{2}$) | C. | ($\frac{3π}{2}$,$\frac{π}{2}$) | D. | (-$\frac{3π}{2}$,-$\frac{π}{2}$) |
分析 先设切点坐标为P(m,n),然后得到两个等式f(m)=n,f'(m)=2,利用f'(m)=2得出sinm=1,排除一些选项,最后根据f(m)=n再排除一些选项即可.
解答 解:直线m:x+2y-3=0斜率为-$\frac{1}{2}$,
若l⊥m,则直线l的斜率为2,
∵函数y=3x+cosx的图象与直线l相切于P点,
设切点坐标为(m,n),
函数y=3x+cosx的导数为y′=3-sinx,
则n=3m+cosm,且f'(m)=3-sinm=2
∴sinm=1,⇒cosm=0,
∴n=3m,
从而排除A,C,D.
故选B.
点评 本题主要考查了利用导数研究曲线上某点切线方程,以及直线的一般式方程与直线的垂直关系,属于基础题.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:选择题
 如图Rt△ABC中,∠ACB=90°,直线l过点A且垂直于平面ABC,动点P∈l,当点P逐渐远离点A时,∠PBC的大小( )
如图Rt△ABC中,∠ACB=90°,直线l过点A且垂直于平面ABC,动点P∈l,当点P逐渐远离点A时,∠PBC的大小( )| A. | 不变 | B. | 变小 | ||
| C. | 变大 | D. | 有时变大有时变小 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
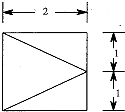 已知四棱锥,它的底面是边长为2的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数有3个,该四棱锥的体积为$\frac{4}{3}$.
已知四棱锥,它的底面是边长为2的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数有3个,该四棱锥的体积为$\frac{4}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )| A. | AC⊥SB | |
| B. | AB∥平面SCD | |
| C. | AC⊥面SBD | |
| D. | AB与SC所成的角等于DC与SA所成的角 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
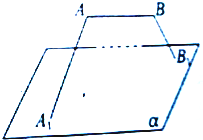 线段AB与平面α平行,α的斜线A1A、B1B与α所成的角分别为30°和60°,且∠A1AB=∠B1BA=90°,AB=2,A1B1=4,求AB与平面α的距离.
线段AB与平面α平行,α的斜线A1A、B1B与α所成的角分别为30°和60°,且∠A1AB=∠B1BA=90°,AB=2,A1B1=4,求AB与平面α的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com