
【题目】已知| ![]() |=1,|
|=1,| ![]() |=
|= ![]() .
.
(1)若 ![]() ∥
∥ ![]() ,求
,求 ![]()
![]() ;
;
(2)若 ![]() ,
, ![]() 的夹角为135°,求|
的夹角为135°,求| ![]() |;
|;
(3)若 ![]() ﹣
﹣ ![]() 与
与 ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角.
的夹角.
科目:高中数学 来源: 题型:
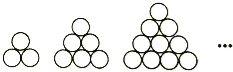
【题目】宋元时期杰出的数学家朱世杰在其数学巨著《四元玉鉴》卷中“茭草形段”第一个问题“今有茭草六百八十束,欲令‘落一形’埵(同垛)之.问底子(每层三角形边茭草束数,等价于层数)几何?”中探讨了“垛枳术”中的落一形垛(“落一形”即是指顶上1束,下一层3束,再下一层6束,…,成三角锥的堆垛,故也称三角垛,如图,表示第二层开始的每层茭草束数),则本问题中三角垛底层茭草总束数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=3sin(2x+ ![]() )的图象,只要把函数y=3sinx的图象上所有的点( )
)的图象,只要把函数y=3sinx的图象上所有的点( )
A.横坐标缩短到原来的 ![]() 倍(纵坐标不变),再把所得图象所有的点向左平移
倍(纵坐标不变),再把所得图象所有的点向左平移 ![]() 个单位长度
个单位长度
B.横坐标伸长到原来的2倍(纵坐标不变),再把所得图象所有的点向左平移 ![]() 个单位长度
个单位长度
C.向右平移 ![]() 个单位长度,再把所得图象所有的点横坐标缩短到原来的
个单位长度,再把所得图象所有的点横坐标缩短到原来的 ![]() 倍(纵坐标不变)
倍(纵坐标不变)
D.向左平移 ![]() 个单位长度,再把所得图象所有的点横坐标伸长到原来的2倍(纵坐标不变)
个单位长度,再把所得图象所有的点横坐标伸长到原来的2倍(纵坐标不变)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,定直线
,定直线![]() :
: ![]() ,动圆
,动圆![]() 过点
过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆![]() 的圆心轨迹
的圆心轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线与曲线
的直线与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,分别过点
两点,分别过点![]() ,
, ![]() 作曲线
作曲线![]() 的切线
的切线![]() ,
, ![]() ,两条切线相交于点
,两条切线相交于点![]() ,求
,求![]() 外接圆面积的最小值.
外接圆面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,设直线
,设直线![]() 的斜率是
的斜率是![]() ,且
,且![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的标准方程.
(Ⅱ)若直线![]() 在
在![]() 轴上的截距是
轴上的截距是![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
(Ⅲ)以![]() 为底作等腰三角形,顶点为
为底作等腰三角形,顶点为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,a,b,c分别是△ABC三个内角A,B,C的对边,下列四个命题:
①若tanA+tanB+tanC>0,则△ABC是锐角三角形
②若acoA=bcosB,则△ABC是等腰三角形
③若bcosC+ccosB=b,则△ABC是等腰三角形
④若 ![]() =
= ![]() ,则△ABC是等边三角形
,则△ABC是等边三角形
其中正确命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com