
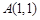 是椭圆
是椭圆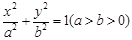 上一点,
上一点, ,
, 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足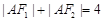
 、
、 是椭圆上任两点,且直线
是椭圆上任两点,且直线 、
、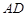 的斜率分别为
的斜率分别为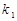 、
、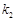 ,若存在常数
,若存在常数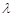 使
使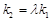 ,求直线
,求直线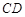 的斜率.
的斜率. 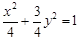 ;(II)
;(II)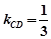 。
。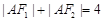 ,可知a=2,所以再把点A的坐标代入椭圆方程求出b的值,求出椭圆的方程.
,可知a=2,所以再把点A的坐标代入椭圆方程求出b的值,求出椭圆的方程.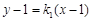 ,由
,由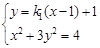 ,得:
,得: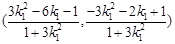 ,同理求出D的坐标,再利用斜率公式即可证明CD的斜率为定值.
,同理求出D的坐标,再利用斜率公式即可证明CD的斜率为定值.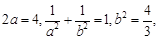 所求椭圆方程
所求椭圆方程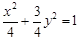 …………………3分;
…………………3分;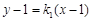 ,由
,由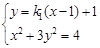 ,得:
,得: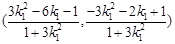 …………………………..5分;
…………………………..5分; 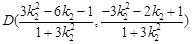 ………………………..6分;
………………………..6分; 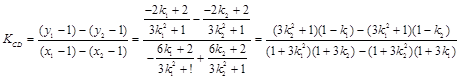
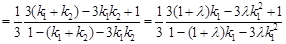 ……………………8分;
……………………8分;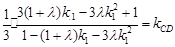 为常数,
为常数,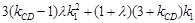 +(1-
+(1-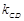 )=0,
)=0,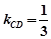 …………………………10分.
…………………………10分. 

科目:高中数学 来源:不详 题型:解答题
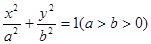 ,离心率为
,离心率为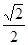 的椭圆经过点
的椭圆经过点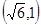 .
.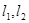 分别与椭圆交于
分别与椭圆交于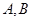 和
和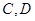 ,是否存在常数
,是否存在常数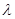 ,使得
,使得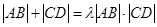 ?若存在,求出实数
?若存在,求出实数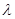 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
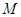 的中心为
的中心为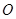 ,长轴的两个端点为
,长轴的两个端点为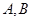 ,右焦点为
,右焦点为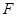 ,
,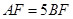 .若椭圆
.若椭圆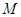 经过点
经过点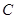 ,
,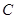 在
在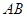 上的射影为
上的射影为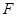 ,且△
,且△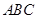 的面积为5.
的面积为5.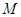 的方程;
的方程;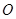 :
: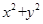 =1,直线
=1,直线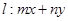 =1,试证明:当点
=1,试证明:当点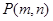 在椭圆
在椭圆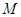 上
上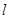 与圆
与圆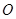 恒相交;并求直线
恒相交;并求直线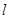 被圆
被圆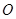 截得的弦长的取值范围.
截得的弦长的取值范围. 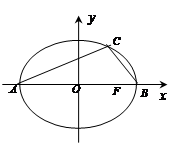
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
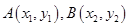 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: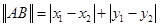 .给出下列三个命题:
.给出下列三个命题: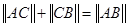 ;
;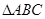 中,若∠C=90°,则
中,若∠C=90°,则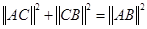 ;
;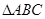 中,
中,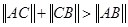 .
.| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com