Question

10．正四棱柱ABCD-A₁B₁C₁D₁中，底面边长为1，侧棱长为2，则异面直线AC₁与B₁C所成角的余弦值是$\frac{\sqrt{30}}{10}$．

Answer 1

分析 以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，利用向量法能求出异面直线AC₁与B₁C所成角的余弦值．

解答 解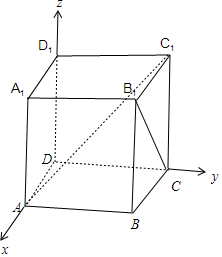：以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，
则A（1，0，0），C₁（0，1，2），B₁（1，1，2），C（0，1，0），
$\overrightarrow{A{C}_{1}}$=（-1，1，2），$\overrightarrow{{B}_{1}C}$=（-1，0，-2），
设异面直线AC₁与B₁C所成角为θ，
则cosθ=$\frac{|\overrightarrow{A{C}_{1}}•\overrightarrow{{B}_{1}C}|}{|\overrightarrow{A{C}_{1}}•\overrightarrow{{B}_{1}C}|}$=$\frac{3}{\sqrt{6}•\sqrt{5}}$=$\frac{\sqrt{30}}{10}$．
∴异面直线AC₁与B₁C所成角的余弦值是$\frac{\sqrt{30}}{10}$．
故答案为：$\frac{\sqrt{30}}{10}$．

点评 本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意向量法的合理运用．