
分析 (1)由已知可得随机变量ξ的值可能为3,4,5,进而可由古典概型概念公式,求出随机变量ξ的分布列,代入数学期望公式,可得数学期望
(2)小王恰好到达6有三种情形,分别求出相对应的概率,根据概率公式计算即可.
解答 解:(1)ξ的可能取值为3,4,5…(1分)$P(ξ=3)=\frac{2}{3}×\frac{2}{3}=\frac{4}{9}$,$P(ξ=4)=C_2^1\frac{2}{3}×\frac{1}{3}=\frac{4}{9}$,$P(ξ=5)=\frac{1}{3}×\frac{1}{3}=\frac{1}{9}$…(4分)
ξ的分布列为
| ξ | 3 | 4 | 5 |
| p | $\frac{4}{9}$ | $\frac{4}{9}$ | $\frac{1}{9}$ |
点评 本题考查的知识点是离散型随机变量的分布列与数学期望,等可能事件的概率,是概率问题的综合应用,难度不大,属于基础题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 家庭月收入 (单位:元) | 2千以下 | 2千~5千 | 5千~8千 | 8千~一万 | 1万~2万 | 2万以上 |
| 调查的总人数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 有二孩计划的家庭数 | 1 | 2 | 9 | 7 | 3 | 4 |
| 收入不高于8千的家庭数 | 收入高于8千的家庭数 | 合计 | |
| 有二孩计划的家庭数 | |||
| 无二孩计划的家庭数 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)关于x=$\frac{5}{9}$π对称 | |
| B. | 函数f(x)向左平移$\frac{π}{18}$个单位后是奇函数 | |
| C. | 函数f(x)关于点($\frac{π}{18}$,0)中心对称 | |
| D. | 函数f(x)在区间[0,$\frac{π}{20}$]上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{3}$ | B. | -$\frac{\sqrt{6}}{3}$ | C. | $±\frac{\sqrt{6}}{3}$ | D. | $±\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
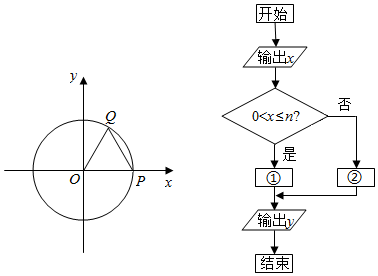
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com