
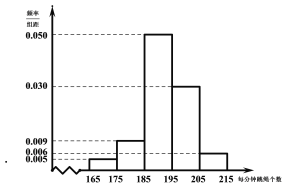
ЁОЬтФПЁПЕБЧАЃЌвдЁАСЂЕТЪїШЫЁБЮЊФПБъЕФПЮГЬИФИяе§дкгаађЭЦНј.ИпжаСЊеаЖдГѕШ§БЯвЕбЇЩњНјааЬхг§ВтЪдЃЌЪЧМЄЗЂбЇЩњЁЂМвГЄКЭбЇаЃЛ§МЋПЊеЙЬхг§ЛюЖЏЃЌБЃжЄбЇЩњНЁПЕГЩГЄЕФгааЇДыЪЉ.ФГЕиЧј2019ФъГѕжаБЯвЕЩњЩ§бЇЬхг§ПМЪдЙцЖЈЃЌПМЩњБиаыВЮМгСЂЖЈЬјдЖЁЂжРЪЕаФЧђЁЂ1ЗжжгЬјЩўШ§ЯюВтЪдЃЌШ§ЯюПМЪдТњЗжЮЊ50ЗжЃЌЦфжаСЂЖЈЬјдЖ15ЗжЃЌжРЪЕаФЧђ15ЗжЃЌ1ЗжжгЬјЩў20Зж.ФГбЇаЃдкГѕШ§ЩЯЦкПЊЪМЪБвЊеЦЮеШЋФъМЖбЇЩњУПЗжжгЬјЩўЕФЧщПіЃЌЫцЛњГщШЁСЫ100УћбЇЩњНјааВтЪдЃЌЕУЕНШчЯТЦЕТЪЗжВМжБЗНЭМЃЌЧвЙцЖЈМЦЗжЙцдђШчЯТБэЃК
УПЗжжгЬј ЩўИіЪ§ |
|
|
|
|
|
ЕУЗж | 16 | 17 | 18 | 19 | 20 |
ЃЈЂёЃЉЯжДгбљБОЕФ100УћбЇЩњжаЃЌШЮвтбЁШЁ2ШЫЃЌЧѓСНШЫЕУЗжжЎКЭВЛДѓгк33ЗжЕФИХТЪЃЛ
ЃЈЂђЃЉШєИУаЃГѕШ§ФъМЖЫљгабЇЩњЕФЬјЩўИіЪ§![]() ЗўДге§ЬЌЗжВМ
ЗўДге§ЬЌЗжВМ![]() ЃЌгУбљБОЪ§ОнЕФЦНОљжЕКЭЗНВюЙРМЦзмЬхЕФЦкЭћКЭЗНВюЃЈНсЙћЫФЩсЮхШыЕНећЪ§ЃЉЃЌвбжЊбљБОЗНВю
ЃЌгУбљБОЪ§ОнЕФЦНОљжЕКЭЗНВюЙРМЦзмЬхЕФЦкЭћКЭЗНВюЃЈНсЙћЫФЩсЮхШыЕНећЪ§ЃЉЃЌвбжЊбљБОЗНВю![]() ЃЈИїзщЪ§ОнгУжаЕужЕДњЬцЃЉ.ИљОнЭљФъОбщЃЌИУаЃГѕШ§ФъМЖбЇЩњОЙ§вЛФъЕФбЕСЗЃЌе§ЪНВтЪдЪБУПШЫУПЗжжгЬјЩўИіЪ§ЖМгаУїЯдНјВНЃЌМйЩшУїФъе§ЪНВтЪдЪБУПШЫУПЗжжгЬјЩўИіЪ§БШГѕШ§ЩЯбЇЦкПЊЪМЪБИіЪ§діМг10ИіЃЌРћгУЯжЫљЕУе§ЬЌЗжВМФЃаЭЃК
ЃЈИїзщЪ§ОнгУжаЕужЕДњЬцЃЉ.ИљОнЭљФъОбщЃЌИУаЃГѕШ§ФъМЖбЇЩњОЙ§вЛФъЕФбЕСЗЃЌе§ЪНВтЪдЪБУПШЫУПЗжжгЬјЩўИіЪ§ЖМгаУїЯдНјВНЃЌМйЩшУїФъе§ЪНВтЪдЪБУПШЫУПЗжжгЬјЩўИіЪ§БШГѕШ§ЩЯбЇЦкПЊЪМЪБИіЪ§діМг10ИіЃЌРћгУЯжЫљЕУе§ЬЌЗжВМФЃаЭЃК
ЃЈЂЁЃЉдЄЙРШЋФъМЖЧЁКУга1000УћбЇЩњЃЌе§ЪНВтЪдЪБУПЗжжгЬј193ИівдЩЯЕФШЫЪ§.ЃЈНсЙћЫФЩсЮхШыЕНећЪ§ЃЉ
ЃЈЂЂЃЉШєдкИУЕиЧј2020ФъЫљгаГѕШ§БЯвЕЩњжаШЮвтбЁШЁ3ШЫЃЌМЧе§ЪНВтЪдЪБУПЗжжгЬј202ИівдЩЯЕФШЫЪ§ЮЊ![]() ЃЌЧѓЫцЛњБфСП
ЃЌЧѓЫцЛњБфСП![]() ЕФЗжВМСаКЭЦкЭћ.
ЕФЗжВМСаКЭЦкЭћ.
ИНЃКШєЫцЛњБфСП![]() ЗўДге§ЬЌЗжВМ
ЗўДге§ЬЌЗжВМ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]()
ЁОД№АИЁПЃЈЂёЃЉ![]() ,ЃЈЂђЃЉЃЈЂЁЃЉ
,ЃЈЂђЃЉЃЈЂЁЃЉ![]() ,ЃЈЂЂЃЉЗжВМСаМћНтЮі ,
,ЃЈЂЂЃЉЗжВМСаМћНтЮі ,![]()
ЁОНтЮіЁП
ЃЈЂёЃЉИљОнЦЕТЪЗжВМжБЗНЭММЦЫуЃЌУПЗжжгЬјЩўИіЪ§![]() ЕФШЫЪ§ЮЊ
ЕФШЫЪ§ЮЊ![]() ЃЈШЫЃЉУПЗжжгЬјЩўИіЪ§
ЃЈШЫЃЉУПЗжжгЬјЩўИіЪ§![]() ЕФШЫЪ§ЮЊ
ЕФШЫЪ§ЮЊ![]() ЃЈШЫЃЉЃЌгЩЬтвтПЩжЊЃЌСНШЫЕУЗжжЎКЭВЛДѓгк33ЗжЃЌМДСНШЫЕУЗжОљЮЊ16ЗжЃЌЛђСНШЫжа1ШЫ16ЗжЃЌ1ШЫ17ЗжЃЌИљОнЛЅГтЪТМўИХТЪМгЗЈЙЋЪНЃЌМЦЫуМДПЩ.
ЃЈШЫЃЉЃЌгЩЬтвтПЩжЊЃЌСНШЫЕУЗжжЎКЭВЛДѓгк33ЗжЃЌМДСНШЫЕУЗжОљЮЊ16ЗжЃЌЛђСНШЫжа1ШЫ16ЗжЃЌ1ШЫ17ЗжЃЌИљОнЛЅГтЪТМўИХТЪМгЗЈЙЋЪНЃЌМЦЫуМДПЩ.
ЃЈЂђЃЉИљОнЦЕТЪЗжВМжБЗНЭММЦЫубљБОЕФОљжЕ![]() ЃЌПЩжЊе§ЪНВтЪдЪБЦкЭћЕФЙРМЦжЕ
ЃЌПЩжЊе§ЪНВтЪдЪБЦкЭћЕФЙРМЦжЕ![]() ЃЌЗНВю
ЃЌЗНВю![]() ЃЌМЦЫу
ЃЌМЦЫу![]() ЃЌ
ЃЌ![]() ЃЌЃЈЂЁЃЉИљОне§ЬЌЗжВМЕФЖдГЦадЃЌМЦЫу
ЃЌЃЈЂЁЃЉИљОне§ЬЌЗжВМЕФЖдГЦадЃЌМЦЫу![]() ЃЌЧѓНтШЫЪ§МДПЩ. ЃЈЂЂЃЉгЩе§ЬЌЗжВМФЃаЭЃЌдкИУЕиЧј2020ФъГѕШ§БЯвЕЩњжаШЮШЁ1ШЫЃЌУПЗжжгЬјЩўИіЪ§202вдЩЯЕФИХТЪЮЊ
ЃЌЧѓНтШЫЪ§МДПЩ. ЃЈЂЂЃЉгЩе§ЬЌЗжВМФЃаЭЃЌдкИУЕиЧј2020ФъГѕШ§БЯвЕЩњжаШЮШЁ1ШЫЃЌУПЗжжгЬјЩўИіЪ§202вдЩЯЕФИХТЪЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЗўДгЖўЯюЗжВМЃЌМД
ЗўДгЖўЯюЗжВМЃЌМД![]() ЃЌМЦЫуЗжВМСаКЭЦкЭћЃЌМДПЩ.
ЃЌМЦЫуЗжВМСаКЭЦкЭћЃЌМДПЩ.
ЃЈЂёЃЉгЩЬтвтПЩжЊЃЌЕУ16ЗжЕФШЫЪ§ЮЊ5ШЫЃЌЕУ17ЗжЕФШЫЪ§ЮЊ9ШЫЃЌСНШЫЕУЗжжЎКЭВЛДѓгк33ЗжЃЌМДСНШЫЕУЗжОљЮЊ16ЗжЃЌЛђСНШЫжа1ШЫ16ЗжЃЌ1ШЫ17Зж.
ЫљвдЃЌСНШЫЕУЗжжЎКЭВЛДѓгк33ЗжЕФИХТЪЮЊЃК![]() .
.
ЃЈЂђЃЉ![]() ЃЈИіЃЉ
ЃЈИіЃЉ
гж![]() ЃЌ
ЃЌ![]() ЃЌЫљвде§ЪНВтЪдЪБЃЌ
ЃЌЫљвде§ЪНВтЪдЪБЃЌ![]() ЃЌ
ЃЌ![]() .
.
Ёр![]() ЃЌ
ЃЌ![]() .
.
ЃЈЂЁЃЉЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЈШЫЃЉ.
ЃЈШЫЃЉ.
ЃЈЂЂЃЉгЩе§ЬЌЗжВМФЃаЭЃЌдкИУЕиЧј2020ФъГѕШ§БЯвЕЩњжаШЮШЁ1ШЫЃЌУПЗжжгЬјЩўИіЪ§202вдЩЯЕФИХТЪЮЊ![]() ЃЌМД
ЃЌМД![]() .
.
Ёр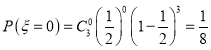 ЃЌ
ЃЌ ЃЌ
ЃЌ
 ЃЌ
ЃЌ ЃЌ
ЃЌ
Ёр![]() ЕФЗжВМСаЮЊ
ЕФЗжВМСаЮЊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() .
.


 ЛЊЖЋЪІДѓАцвЛПЮвЛСЗЯЕСаД№АИ
ЛЊЖЋЪІДѓАцвЛПЮвЛСЗЯЕСаД№АИ УЯНЈЦНУћаЃПМОэЯЕСаД№АИ
УЯНЈЦНУћаЃПМОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉШє![]() ЃЌЧв
ЃЌЧв![]() дк
дк![]() ЩЯДцдкСуЕуЃЌЧѓЪЕЪ§
ЩЯДцдкСуЕуЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєЖдШЮвт![]() ЃЌДцдк
ЃЌДцдк![]() ЪЙ
ЪЙ![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШєДцдкЪЕЪ§![]() ЃЌЪЙЕУЕБ
ЃЌЪЙЕУЕБ![]() ЪБЃЌ
ЪБЃЌ![]() КуГЩСЂЃЌЧѓЪЕЪ§
КуГЩСЂЃЌЧѓЪЕЪ§![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌНЧAЃЌBЃЌCЕФЖдБпЗжБ№ЮЊaЃЌbЃЌcЃЌЧв2acosBЃН2cЉbЃЎ
ЃЈ1ЃЉЧѓЁЯAЕФДѓаЁЃЛ
ЃЈ2ЃЉШєЁїABCЕФЭтНгдВЕФАыОЖЮЊ![]() ЃЌУцЛ§ЮЊ
ЃЌУцЛ§ЮЊ![]() ЃЌЧѓЁїABCЕФжмГЄЃЎ
ЃЌЧѓЁїABCЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпy=x2Љ2xsinІС+1ЕФЖЅЕудкЭждВx2+my2=1ЩЯЃЌетбљЕФХзЮяЯпгаЧвжЛгаСНЬѕЃЌдђmЕФШЁжЕЗЖЮЇЪЧ_____.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕШВюЪ§Са{bn}ЕФЧАnЯюКЭЮЊTnЃЌЧвT4=4ЃЌb5=6.
ЃЈ1ЃЉЧѓЪ§Са{bn}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉШєе§ећЪ§n1ЃЌn2ЃЌЁЃЌntЃЌЁТњзу5ЃМn1ЃМn2ЃМЁЃМntЃЌЁЧвb3ЃЌb5ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЃЌЁГЩЕШБШЪ§СаЃЌЧѓЪ§Са{nt}ЕФЭЈЯюЙЋЪНЃЈtЪЧе§ећЪ§ЃЉЃЛ
ЃЌЁГЩЕШБШЪ§СаЃЌЧѓЪ§Са{nt}ЕФЭЈЯюЙЋЪНЃЈtЪЧе§ећЪ§ЃЉЃЛ
ЃЈ3ЃЉИјГіУќЬтЃКдкЙЋБШВЛЕШгк1ЕФЕШБШЪ§Са{an}жаЃЌЧАnЯюКЭЮЊSnЃЌШєamЃЌam+2ЃЌam+1ГЩЕШВюЪ§СаЃЌдђSmЃЌSm+2ЃЌSm+1вВГЩЕШВюЪ§Са.ЪдХаЖЯДЫУќЬтЕФецМйЃЌВЂжЄУїФуЕФНсТл.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃК
ЃК![]() Й§Еу
Й§Еу![]() ЃЌЙ§зјБъдЕу
ЃЌЙ§зјБъдЕу![]() зїСНЬѕЛЅЯрДЙжБЕФЩфЯпгыЭждВ
зїСНЬѕЛЅЯрДЙжБЕФЩфЯпгыЭждВ![]() ЗжБ№НЛгк
ЗжБ№НЛгк![]() ЃЌ
ЃЌ![]() СНЕу.
СНЕу.
ЃЈ1ЃЉжЄУїЃКЕБ![]() ШЁЕУзюаЁжЕЪБЃЌЭждВ
ШЁЕУзюаЁжЕЪБЃЌЭждВ![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ![]() .
.
ЃЈ2ЃЉШєЭждВ![]() ЕФНЙОрЮЊ2ЃЌЪЧЗёДцдкЖЈдВгыжБЯп
ЕФНЙОрЮЊ2ЃЌЪЧЗёДцдкЖЈдВгыжБЯп![]() змЯрЧаЃПШєДцдкЃЌЧѓЖЈдВЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
змЯрЧаЃПШєДцдкЃЌЧѓЖЈдВЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХН№ШкЪаГЁЕФЗЂеЙЃЌдНРДдНЖрШЫбЁдёЭЖзЪЁАЛЦН№ЁБзїЮЊРэВЦЕФЪжЖЮЃЌЯТУцНЋAЪаАбЛЦН№зїЮЊРэВЦВњЦЗЕФЭЖзЪШЫЕФФъСфЧщПіЭГМЦШчЯТЭМЫљЪО.
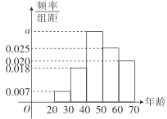
ЃЈ1ЃЉЧѓАбЛЦН№зїЮЊРэВЦВњЦЗЕФЭЖзЪепЕФФъСфЕФжаЮЛЪ§ЃЛЃЈНсЙћгУаЁЪ§БэЪОЃЌаЁЪ§ЕуКѓБЃСєСНЮЛгааЇЪ§зжЃЉ
ЃЈ2ЃЉЯжАДееЗжВуГщбљЕФЗНЗЈДгФъСфдк![]() КЭ
КЭ![]() ЕФЭЖзЪепжаЫцЛњГщШЁ5ШЫЃЌдйДгет5ШЫжаЫцЛњГщШЁ3ШЫНјааЭЖзЪЕїВщЃЌЧѓЧЁга1ШЫФъСфдк
ЕФЭЖзЪепжаЫцЛњГщШЁ5ШЫЃЌдйДгет5ШЫжаЫцЛњГщШЁ3ШЫНјааЭЖзЪЕїВщЃЌЧѓЧЁга1ШЫФъСфдк![]() ЕФИХТЪ.
ЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌгЩАыдВ![]() КЭВПЗжХзЮяЯп
КЭВПЗжХзЮяЯп![]() КЯГЩЕФЧњЯп
КЯГЩЕФЧњЯп![]() ГЦЮЊЁАг№УЋЧђПЊЯпЁБЃЌЧњЯп
ГЦЮЊЁАг№УЋЧђПЊЯпЁБЃЌЧњЯп![]() гы
гы![]() жсга
жсга![]() СНИіНЙЕуЃЌЧвОЙ§Еу
СНИіНЙЕуЃЌЧвОЙ§Еу![]()

(1)Чѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
(2)Щш![]()
![]() ЮЊЧњЯп
ЮЊЧњЯп![]() ЩЯЕФЖЏЕуЃЌЧѓ
ЩЯЕФЖЏЕуЃЌЧѓ![]() ЕФзюаЁжЕЃЛ
ЕФзюаЁжЕЃЛ
(3)Й§![]() ЧваБТЪЮЊ
ЧваБТЪЮЊ![]() ЕФжБЯп
ЕФжБЯп![]() гыЁАг№УЋЧђаЮЯпЁБЯрНЛгкЕу
гыЁАг№УЋЧђаЮЯпЁБЯрНЛгкЕу![]() Ш§ЕуЃЌЮЪЪЧЗёДцдкЪЕЪ§
Ш§ЕуЃЌЮЪЪЧЗёДцдкЪЕЪ§![]() ЪЙЕУ
ЪЙЕУ![]() ЃПШєДцдкЃЌЧѓГі
ЃПШєДцдкЃЌЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкКЏЪ§![]() ЖЈвх
ЖЈвх![]() вбжЊХМКЏЪ§
вбжЊХМКЏЪ§![]() ЕФЖЈвхгђЮЊ
ЕФЖЈвхгђЮЊ![]() ЕБ
ЕБ![]() Чв
Чв![]() ЪБЃЌ
ЪБЃЌ![]()
ЃЈ1ЃЉЧѓ![]() ВЂЧѓГіКЏЪ§
ВЂЧѓГіКЏЪ§![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєДцдкЪЕЪ§![]() ЪЙЕУКЏЪ§
ЪЙЕУКЏЪ§![]() дк
дк![]() ЩЯЕФжЕгђЮЊ
ЩЯЕФжЕгђЮЊ![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com