Question

4．已知函数f（x）=$\left\{\begin{array}{l}{ax+1（x≤0）}\\{lo{g}_{2}x（x＞0）}\end{array}\right.$，若函数y=f[f（x）]+1有4个不同的零点，则实数a的取值范围是（0，+∞）．

Answer 1

分析 函数y=f[f（x）]+1的零点个数，即为方程f[f（x）]=-1的解的个数，结合函数f（x）图象，分类讨论判断，求解方程可得答案．

解答 解：函数y=f（f（x））+1的零点，
即方程f[f（x）]=-1的解个数，
（1）当a=0时，f（x）=$\left\{\begin{array}{l}1（x≤0）\\ lo{g}_{2}x（x＞0）\end{array}\right.$，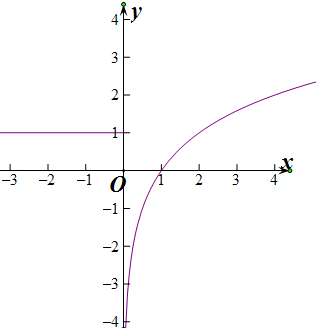

当x＞1时，x=$\sqrt{2}$，f（f（x））=-1成立，∴方程f[f（x）]=-1有1解
当0＜x＜1，log₂x＜0，∴方程f[f（x）]=-1无解，
当x≤0时，f（x）=1，f（f（x））=0，∴f（f（x））=-1有1解，
故a=0不符合题意，
（2）当a＞0时，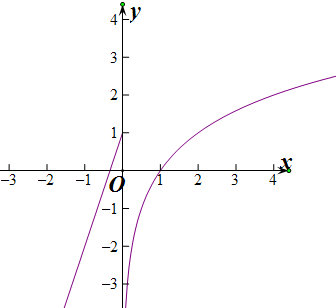

当x＞1时，x=$\sqrt{2}$，f（f（x））=-1成立，
当0＜x＜1，log₂x＜0，∴方程f[f（x）]=-1有1解，
当$\frac{1}{a}$＜x≤0时，0＜f（x）≤1，∴f（f（x））=-1有1解，
当x≤-$\frac{1}{a}$时，f（x）＜0，∴f（f（x））=-1有1解，
故f（f（x））=-1有4解，
（3）当a＜0时，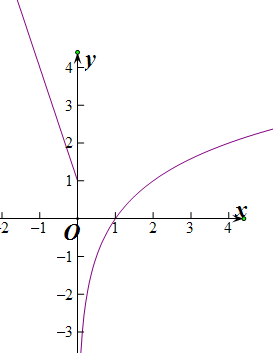

当x＞1时，x=$\sqrt{2}$，f（f（x））=-1成立，∴f（f（x））=-1有1解，
当0＜x≤1时，f（x）≤0．f（f（x））=-1，成立∴f（f（x））=-1有1解，
当x≤0时，f（x）≥1，f（f（x））=-1，成立∴f（f（x））=-1有1解，
故f（f（x））=-1有3解，
不符合题意，
综上；a＞0
故答案为：（0，+∞）

点评 本题考查的知识点是函数零点的判定，其中将函数的零点问题转化为方程根的个数问题，分类讨论求解．