
分析 (1)利用递推关系与等比数列的通项公式即可证明.
(2)当n≥2时,bn=$\frac{9×3×{4}^{n-2}}{(3×{4}^{n-2}+3)(3×{4}^{n-1}+3)}$=$\frac{3×{4}^{n-2}}{({4}^{n-2}+1)({4}^{n-1}+1)}$,又${b}_{1}=\frac{3}{8}$.利用“裂项求和”方法即可得出.
解答 (1)证明:当n≥2时,an+1Sn-1-anSn=0.
∴${a_{n+1}}{S_{n-1}}-{a_n}{S_n}=({{S_{n+1}}-{S_n}}){S_{n-1}}-({{S_n}-{S_{n-1}}}){S_n}={S_{n+1}}{S_{n-1}}-S_n^2=0$,
∴$S_n^2={S_{n-1}}{S_{n+1}}({n≥2})$,
又由S1=1≠0,S2=4≠0,
可推知对一切正整数n均有Sn≠0,则数列{Sn}是等比数列,公比q=$\frac{{S}_{2}}{{S}_{1}}$=4,首项为1.
∴${S_n}={4^{n-1}}$.
当n≥2时,an=Sn-Sn-1=3×4n-2,又a1=S1=1,
∴an=$\left\{\begin{array}{l}{1,n=1}\\{3×{4}^{n-2},n≥2}\end{array}\right.$.
(2)解:当n≥2时,bn=$\frac{{9{a_n}}}{{({{a_n}+3})({{a_{n+1}}+3})}}$=$\frac{9×3×{4}^{n-2}}{(3×{4}^{n-2}+3)(3×{4}^{n-1}+3)}$=$\frac{3×{4}^{n-2}}{({4}^{n-2}+1)({4}^{n-1}+1)}$,又${b}_{1}=\frac{3}{8}$.
∴${b_n}=\left\{{\begin{array}{l}{\frac{3}{8},({n=1})}\\{\frac{{3×{4^{n-2}}}}{{({{4^{n-2}}+1})({{4^{n-1}}+1})}},({n≥2})}\end{array}}\right.$,
则${T_1}={b_1}=\frac{3}{8}$,
当n≥2时,bn=$\frac{1}{{4}^{n-2}+1}-\frac{1}{{4}^{n-1}+1}$,
则${T_n}=\frac{3}{8}+({\frac{1}{{{4^{2-2}}+1}}-\frac{1}{{{4^{2-1}}+1}}})+…+({\frac{1}{{{4^{n-2}}+1}}-\frac{1}{{{4^{n-1}}+1}}})=\frac{7}{8}-\frac{1}{{{4^{n-1}}+1}}$,
n=1时也成立.
综上:${T_n}=\frac{7}{8}-\frac{1}{{{4^{n-1}}+1}}$.
点评 本题考查了递推关系、等比数列的通项公式、“裂项求和”方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)与g(x)的最大值不同 | |
| B. | 函数f(x)与g(x)在$(\frac{3π}{4},\;\;\frac{5π}{4})$上都为增函数 | |
| C. | 函数f(x)与g(x)的图象的对称轴相同 | |
| D. | 将函数f(x)的图象上各点的横坐标缩短为原来的$\frac{1}{2}$,纵坐标不变,再通过平移能得到g(x)的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{5}{9}$ | C. | 1 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
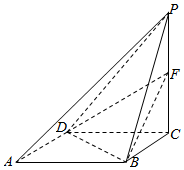 在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PC⊥平面ABCD,且AB=2,PC=$\sqrt{6}$,F是PC的中点.
在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PC⊥平面ABCD,且AB=2,PC=$\sqrt{6}$,F是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
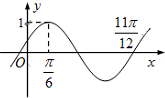 函数f(x)=Asin(wx+φ)(A>0,w>0,φ∈R)的部分图象如图所示,则将y=f(x)的图象向右平移π6个单位后得到g(x),得到的函数图象对称轴为x=$\frac{kπ}{2}$+$\frac{π}{3}$,k∈Z,函数g(x)的解析式为y=sin(2x-$\frac{π}{6}$).
函数f(x)=Asin(wx+φ)(A>0,w>0,φ∈R)的部分图象如图所示,则将y=f(x)的图象向右平移π6个单位后得到g(x),得到的函数图象对称轴为x=$\frac{kπ}{2}$+$\frac{π}{3}$,k∈Z,函数g(x)的解析式为y=sin(2x-$\frac{π}{6}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 甲 | 11.6 | 12.2 | 13.2 | 13.9 | 14.0 | 11.5 | 13.1 | 14.5 | 11.7 | 14.3 |
| 乙 | 12.3 | 13.3 | 14.3 | 11.7 | 12.0 | 12.8 | 13.2 | 13.8 | 14.1 | 12.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 6或14 | C. | 14 | D. | 2或18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com