
| A. | 6 | B. | 6或14 | C. | 14 | D. | 2或18 |
分析 求得抛物线的焦点和准线方程,运用抛物线的定义可得|MN|=|FM|=10,求得M的横坐标,再由直角三角形的性质:斜边的中线为斜边的一半,以及中点坐标公式可得圆C2的圆心为(5,3),求得M(10-$\frac{p}{2}$,6),代入抛物线的方程,解得p的值,即可得到所求距离.
解答  解:抛物线C1:y2=2px(p>0)的焦点为($\frac{p}{2}$,0),
解:抛物线C1:y2=2px(p>0)的焦点为($\frac{p}{2}$,0),
准线为l:x=-$\frac{p}{2}$,
由|FM|=10,由抛物线的定义可得|MN|=|FM|=10,
即有xM+$\frac{p}{2}$=10,即xM=10-$\frac{p}{2}$,
以线段FM为直径的圆C2过点A(0,3),
连接AM,AF,可得|AC2|=$\frac{1}{2}$|FM|=5,
可得圆C2的圆心为(5,3),
由中点坐标公式可得M(10-$\frac{p}{2}$,6),
代入抛物线的方程可得36=2p(10-$\frac{p}{2}$),
解得p=2或18.
则圆心C2到抛物线的准线的距离为5+$\frac{p}{2}$
=5+1=6或5+9=14.
故选:B.
点评 本题考查抛物线的定义、方程和性质,注意运用定义法解题,考查直角三角形的性质:斜边的中线为斜边的一半,考查运算能力,属于中档题.


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b-1 | B. | a>b+1 | C. | a2>b2 | D. | $\frac{1}{a}$<$\frac{1}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p | B. | ¬q | C. | (¬p)∧q | D. | p∨(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.3 | B. | 0.5 | C. | 0.1 | D. | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,3,4,5} | B. | {2,3,4} | C. | {3,4,5} | D. | {2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
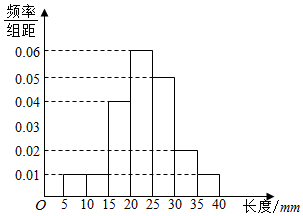 某棉纺厂为了了解一批棉花的质量,从中随机抽测了100根棉花纤维的长度(棉花纤维所得数据均在区间[5,40]中,其频率分布直方图如图所示,则在抽测的100根中10根棉花纤维的长度小于15mm.
某棉纺厂为了了解一批棉花的质量,从中随机抽测了100根棉花纤维的长度(棉花纤维所得数据均在区间[5,40]中,其频率分布直方图如图所示,则在抽测的100根中10根棉花纤维的长度小于15mm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com