
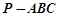 中,
中,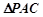 ,
,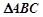 是等边三角形.
是等边三角形.
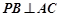 ;
;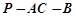 的大小为
的大小为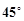 ,求
,求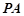 与平面
与平面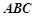 所成角的正弦值.
所成角的正弦值.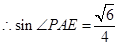 .
. ,只需证明一条直线垂直于另一条直线所在的平面,注意到
,只需证明一条直线垂直于另一条直线所在的平面,注意到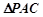 ,
,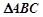 是等边三角形,可考虑取
是等边三角形,可考虑取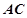 的中点
的中点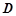 ,连接
,连接 ,只需证
,只需证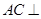 面
面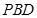 即可,显然易证,从而可得
即可,显然易证,从而可得 ;(II)若二面角
;(II)若二面角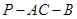 的大小为
的大小为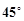 ,求
,求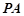 与平面
与平面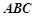 所成角的正弦值,首先确定二面角
所成角的正弦值,首先确定二面角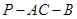 的平面角,由(I)可知,
的平面角,由(I)可知,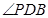 即为二面角
即为二面角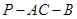 的平面角,所以
的平面角,所以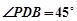 ,求
,求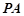 与平面
与平面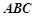 所成角的正弦值,关键是找
所成角的正弦值,关键是找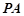 在平面
在平面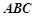 上的射影,注意到平面
上的射影,注意到平面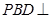 平面
平面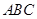 ,可过点
,可过点 作
作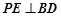 ,则
,则 面
面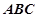 ,则
,则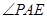 为
为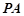 与平面
与平面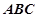 所成角,为了便于计算,可设
所成角,为了便于计算,可设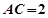 ,从而求出
,从而求出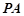 与平面
与平面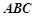 所成角的正弦值.
所成角的正弦值.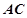 的中点
的中点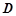 ,连接
,连接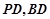 . 2分
. 2分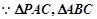 是等边三角形,
是等边三角形,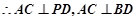 , 4分
, 4分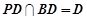 ,
,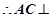 面
面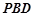 ,
,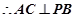 6分
6分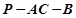 的平面角为
的平面角为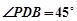 , 8分
, 8分 作
作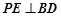 ,由(I)知
,由(I)知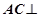 面
面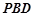 ,
,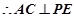 , 又
, 又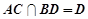 ,
,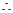
 面
面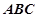 , 10分
, 10分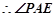 为
为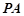 与平面
与平面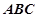 所成角, 11分
所成角, 11分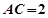 ,则
,则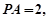
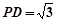 ,
,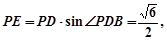
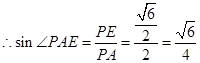 . 14分
. 14分

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,且AB=2AD=2DC=2PD=4,E为PA的中点.
,且AB=2AD=2DC=2PD=4,E为PA的中点.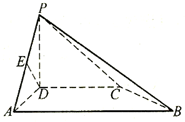
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
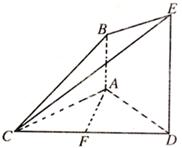
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
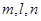 和平面
和平面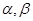 的四个命题:
的四个命题: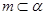 ,
,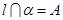 ,点
,点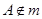 ,则
,则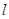 与
与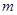 不共面;
不共面;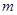 、
、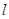 是异面直线,
是异面直线,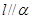 ,
,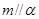 ,且
,且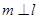 ,
,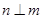 ,则
,则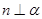 ;
;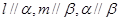 ,则
,则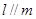 ;
;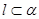 ,
,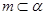 ,
,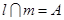 ,
,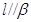 ,
,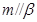 ,则
,则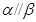 .
.| A.① | B.② | C.④ | D.③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.若任意四点不共面,则其中任意三点必不共线 |
B.若直线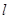 上有一点在平面 上有一点在平面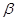 外,则 外,则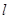 在平面 在平面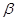 外 外 |
| C.若一个平面内的任一条直线都平行于另一个平面,则这两个平面平行 |
D.若直线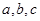 中, 中,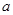 与 与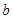 共面且 共面且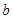 与 与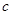 共面,则 共面,则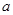 与 与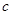 共面 共面 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
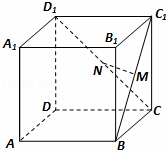
| A.MN与CC1垂直 | B.MN与AC垂直 | C.MN与BD平行 | D.MN与A1B1平行 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
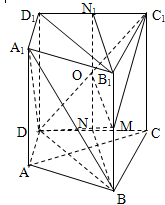
 中,点
中,点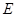 为
为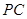 中点,则下列命题正确的是( )
中点,则下列命题正确的是( )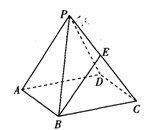
A.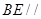 面 面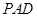 ,且直线 ,且直线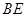 到面 到面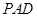 距离为 距离为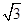 |
B.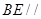 面 面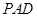 ,且直线 ,且直线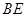 到面 到面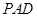 距离为 距离为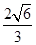 |
C.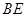 不平行于面 不平行于面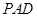 ,且 ,且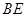 与平面 与平面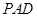 所成角大于 所成角大于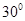 |
D.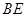 不平行于面 不平行于面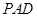 ,且 ,且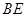 与平面 与平面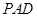 所成角小于 所成角小于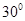 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com