
分析 (1)求出导数,求得切线的斜率和切点,由切线与2x-y=0垂直,可得a,b的方程,解方程可得a,b的值;
(2)由题意可得$\frac{x}{1+{e}^{x}}$+e-x>$\frac{x}{{e}^{x}-1}$+ke-x,即有(1-k)e-x>$\frac{2x}{{e}^{2x}-1}$,即1-k>$\frac{2x}{{e}^{x}-{e}^{-x}}$,可令g(x)=$\frac{2x}{{e}^{x}-{e}^{-x}}$,求出导数,判断单调性,可得最值,即可得到k的范围.
解答 解:(1)f(x)=$\frac{ax}{{e}^{x}+1}$+be-x的导数为
f′(x)=$\frac{a({e}^{x}+1)-ax{e}^{x}}{({e}^{x}+1)^{2}}$,
由切线与直线2x-y=0垂直,可得
f(0)=1,f′(0)=-$\frac{1}{2}$,
即有b=1,$\frac{1}{2}$a-b=-$\frac{1}{2}$,
解得a=b=1;
(2)当x≠0时,都有f(x)>$\frac{x}{{e}^{x}-1}$+ke-x,
即为$\frac{x}{1+{e}^{x}}$+e-x>$\frac{x}{{e}^{x}-1}$+ke-x,
即有(1-k)e-x>$\frac{2x}{{e}^{2x}-1}$,即1-k>$\frac{2x}{{e}^{x}-{e}^{-x}}$,
可令g(x)=$\frac{2x}{{e}^{x}-{e}^{-x}}$,g(-x)=$\frac{-2x}{{e}^{-x}-{e}^{x}}$=g(x),
即有g(x)为偶函数,只要考虑x>0的情况.
由g(x)-1=$\frac{2x-{e}^{x}-{e}^{-x}}{{e}^{x}-{e}^{-x}}$,
x>0时,ex>e-x,
由h(x)=2x-ex+e-x,h′(x)=2-(ex+e-x)≤2-2$\sqrt{{e}^{x}•{e}^{-x}}$=0,
则h(x)在x>0递减,即有h(x)<h(0)=0,
即有g(x)<1.
故1-k≥1,解得k≤0.
则k的取值范围为(-∞,0].
点评 本题考查导数的运用:求切线的斜率和单调性,考查不等式恒成立问题的解法,注意运用参数分离和构造函数,求出导数,判断单调性,求出最值,考查运算能力,属于中档题.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 18 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{4}{5}$ | C. | -4 | D. | -$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
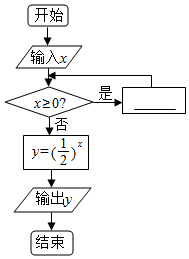 已知①x=x-1,②x=x-2,③x=x-3,④x=x-4在如图所示的程序框图中,如果输入x=10,而输出y=4,则在空白处可填入( )
已知①x=x-1,②x=x-2,③x=x-3,④x=x-4在如图所示的程序框图中,如果输入x=10,而输出y=4,则在空白处可填入( )| A. | ①②③ | B. | ②③ | C. | ③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com