
分析 由已知和正余弦定理可得abc的关系,再由余弦定理可得cosB,由同角三角函数基本关系可得sinB.
解答 解:∵在△ABC中,asinAsinB+bcos2A=$\sqrt{2}$a,
∴由正弦定理得$sinB({sin^2}A+{cos^2}A)=\sqrt{2}sinA$,
化简可得sinB=$\sqrt{2}$sinA,∴b=$\sqrt{2}$a,
又${c^2}={b^2}+\sqrt{3}{a^2}$,∴${c^2}=(2+\sqrt{3}){a^2}$,
故可设$a=1\;,\;\;b=\sqrt{2}\;,\;\;c=\sqrt{2+\sqrt{3}}=\frac{{\sqrt{3}+1}}{{\sqrt{2}}}$,
∴由余弦定理可得$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{{1+2+\sqrt{3}-2}}{{2×1×\frac{{\sqrt{3}+1}}{{\sqrt{2}}}}}=\frac{{\sqrt{2}}}{2}$,
由同角三角函数基本关系可得sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{{\sqrt{2}}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查正余弦定理解三角形,涉及同角三角函数基本关系,属中档题.


 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:解答题
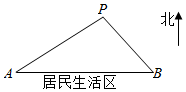 如图所示,A,B是两个垃圾中转站,B在A的正东方向16千米处,AB的南面为居民生活区,为了妥善处理生活垃圾,政府决定在AB的背面建一个垃圾发电厂P,垃圾发电厂P的选址拟满足以下两个要求(A,B,P可看成三个点):
如图所示,A,B是两个垃圾中转站,B在A的正东方向16千米处,AB的南面为居民生活区,为了妥善处理生活垃圾,政府决定在AB的背面建一个垃圾发电厂P,垃圾发电厂P的选址拟满足以下两个要求(A,B,P可看成三个点):查看答案和解析>>
科目:高中数学 来源: 题型:选择题
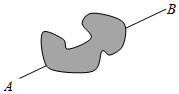 如图所示,为了测量某湖泊两侧A,B间的距离,李宁同学首先选定了与A,B不共线的一点C,然后给出了三种测量方案:(△ABC的角A,B,C所对的边分别记为a,b,c):
如图所示,为了测量某湖泊两侧A,B间的距离,李宁同学首先选定了与A,B不共线的一点C,然后给出了三种测量方案:(△ABC的角A,B,C所对的边分别记为a,b,c):| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,0] | C. | [0,+∞) | D. | (0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com