练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    由1开始的奇数列，按下列方法分组：(1)，(3,5)，(7,9,11)，…，第n组有n个数，则第n组的首项为(　　)

    A．n2－n                                                       B．n2－n＋1

    C．n2＋n                                                       D．n2＋n＋1


    　B


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知△ABC中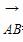，＝a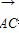，＝b，a·b<0，S△ABC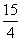＝，|a|＝3，|b|＝5，则∠BAC等于(　　)

    A．30°                                                          B．120°

    C．150°                                                        D．30°或150°

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，△ABC的外接圆的圆心为O，AB＝3，AC＝5，BC＝，则等于(　　)

    A．－8  B．－1  C．1  D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知x与函数f(x)的对应关系如下表所示，数列{an}满足：a1＝3，an＋1＝f(an)，则a2014＝(　　)

    x

    1

    2

    3

    f(x)

    2

    3

    1

    A.3　　　　B．2　　　　C．1　　　　D．不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    正项数列{an}满足：a－(2n－1)an－2n＝0.

    (1)求数列{an}的通项公式an；

    (2)令bn＝，求数列{bn}的前n项和Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项和为Sn，且Sn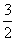＝an－1(n∈N*)．

    (1)求数列{an}的通项公式；

    (2)在数列{bn}中，b1＝5，bn＋1＝bn＋an，求数列{bn}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等差数列{an}的前n项和为Sn，若a3＋a4＋a5＝12，则S7的值为(　　)

    A．28  B．42  C．56  D．14

    查看答案和解析>>

    科目：高中数学 来源： 题型：


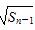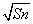    已知每项均大于零的数列{an}中，首项a1＝1且前n项和Sn满足Sn－Sn－1＝2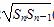 (n∈N*且n≥2)，则a81＝(　　)

    A．641  B．640  C．639  D．638

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项和为Sn，且Sn＝4an－3(n∈N*)．

    (1)证明：数列{an}是等比数列；

    (2)若数列{bn}满足bn＋1＝an＋bn(n∈N*)，且b1＝2，求数列{bn}的通项公式．

    查看答案和解析>>

    同步练习册答案