
已知数列{an}的前n项和为Sn,且Sn=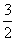 an-1(n∈N*).
an-1(n∈N*).
(1)求数列{an}的通项公式;
(2)在数列{bn}中,b1=5,bn+1=bn+an,求数列{bn}的通项公式.
(1)当n=1时,S1=a1=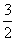 a1-1,所以a1=2.
a1-1,所以a1=2.
∵Sn=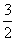 an-1,①
an-1,①
∴当n≥2时,Sn-1=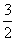 an-1-1,②
an-1-1,②
①-②,得an=(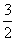 an-1)-(
an-1)-(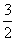 an-1-1),
an-1-1),
所以an=3an-1,又a1≠0,故an-1≠0,
所以 =3,
=3,
故数列{an}是首项为2,公比为3的等比数列,
所以an=2·3n-1.
(2)由(1)知bn+1=bn+2·3n-1.
当n≥2时,bn=bn-1+2·3n-2,
…
b3=b2+2·31,
b2=b1+2·30,
将以上n-1个式子相加并整理,得bn=b1+2×(3n-2+…+31+30)=5+2×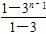 =3n-1+4.
=3n-1+4.
当n=1时,31-1+4=5=b1,
所以bn=3n-1+4(n∈N*).


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
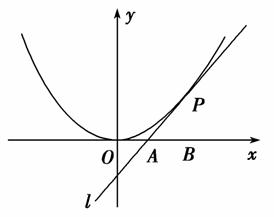
(1)若动点M满足 =0,求点M的轨迹C;
=0,求点M的轨迹C;
(2)若过点B的直线l′(斜率不等于零)与(1)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
由1开始的奇数列,按下列方法分组:(1),(3,5),(7,9,11),…,第n组有n个数,则第n组的首项为( )
A.n2-n B.n2-n+1
C.n2+n D.n2+n+1
查看答案和解析>>
科目:高中数学 来源: 题型:
已知等差数列{an}的前n项和为Sn,若M、N、P三点共线,O为坐标原点,且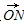 =a15
=a15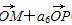 (直线MP不过点O),则S20等于( )
(直线MP不过点O),则S20等于( )
A.10 B.15 C.20 D.40
查看答案和解析>>
科目:高中数学 来源: 题型:
如表定义函数f(x):
| x | 1 | 2 | 3 | 4 | 5 |
| f(x) | 5 | 4 | 3 | 1 | 2 |
对于数列{an},a1=4,an=f(an-1),n=2,3,4,…,则a2014的值是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com