
已知数列{an}的前n项和为Sn,且Sn=4an-3(n∈N*).
(1)证明:数列{an}是等比数列;
(2)若数列{bn}满足bn+1=an+bn(n∈N*),且b1=2,求数列{bn}的通项公式.
科目:高中数学 来源: 题型:
由1开始的奇数列,按下列方法分组:(1),(3,5),(7,9,11),…,第n组有n个数,则第n组的首项为( )
A.n2-n B.n2-n+1
C.n2+n D.n2+n+1
查看答案和解析>>
科目:高中数学 来源: 题型:
已知等比数列{an}满足an+1+an=9·2n-1,n∈N.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,若不等式Sn>kan-2对一切n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
小王每月除去所有日常开支,大约结余a元.小王决定采用零存整取的方式把余钱积蓄起来,每月初存入银行a元,存期1年(存12次),到期取出本和息.假设一年期零存整取的月利率为r,每期存款按单利计息.那么,小王存款到期利息为________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
在如图所示的数表中,第i行第j列的数记为ai,j,且满足a1,j=2j-1,ai,1=i,ai+1,j+1=ai,j+ai+1,j(i,j∈N*);又记第3行的3,5,8,13,22,39,…,为数列{bn},则
| 第1行 | 1 | 2 | 4 | 8 | … |
| 第2行 | 2 | 3 | 5 | 9 | … |
| 第3行 | 3 | 5 | 8 | 13 | … |
| …… |
(1)此数表中的第2行第8列的数为________;
(2)数列{bn}的通项公式为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列不等式一定成立的是( )
A.lg(x2+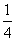 )>lgx(x>0)
)>lgx(x>0)
B.sinx+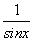 ≥2(x≠kπ,k∈Z)
≥2(x≠kπ,k∈Z)
C.x2+1≥2|x|(x∈R)
D. 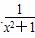 >1(x∈R)
>1(x∈R)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com