练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．某校为了解1000名高一新生的身体生长状况，用系统抽样法（按等距的规则）抽取40名同学进行检查，将学生从1～1000进行编号，现已知第18组抽取的号码为443，则第一组用简单随机抽样抽取的号码为18．

    分析 根据系统抽样的特征，从1000名学生从中抽取一个容量为40的样本，抽样的分段间隔为$\frac{1000}{40}$=25，结合从第18组抽取的号码为443，可得第一组用简单随机抽样抽取的号码．

    解答 解：∵从1000名学生从中抽取一个容量为40的样本，
    ∴系统抽样的分段间隔为$\frac{1000}{40}$=25，
    设第一部分随机抽取一个号码为x，
    则抽取的第18编号为x+17×25=443，∴x=18．
    故答案为18．

    点评 本题考查了系统抽样方法，关键是求得系统抽样的分段间隔．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．若将函数f（x）=sin（2x+$\frac{π}{6}$）的图象向左平移$\frac{π}{4}$个单位长度，再向下平移1个单位长度，得到函数g（x）的图象，则g（x）的一个对称中心为（　　）
    A．（$\frac{π}{6}$，-1）B．（$\frac{π}{3}$，-1）C．（$\frac{π}{6}$，0）D．（$\frac{π}{3}$，0）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．设函数g（x）是R上的偶函数，当x＜0时，g（x）=ln（1-x），函数$f（x）=\left\{\begin{array}{l}{x^3}，x≤0\\ g（x），x＞0\end{array}\right.$满足f（2-x2）＞f（x），则实数x的取值范围是（　　）
    A．（-∞，1）∪（2，+∞）B．（-∞，-2）∪（1，+∞）C．（1，2）D．（-2，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知向量$\overrightarrow a\;，\;\;\overrightarrow b$都是非零向量，“$\overrightarrow a•\overrightarrow b=|{\overrightarrow a}|•|{\overrightarrow b}|$”是“$\overrightarrow a∥\overrightarrow b$”的（　　）
    A．充分非必要条件B．必要非充分条件
    C．充分必要条件D．既非充分也非必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．下列四个函数中是R上的减函数的为（　　）
    A．$y={log_2}{2^{-x}}$B．$y={（{\frac{1}{2}}）^{-x}}$C．$y=\frac{1}{x+1}$D．y=x2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．进位制是人们为了计数和运算方便而约定的记数系统，在日常生活中，我们最熟悉、最常用的是十进制．如图是实现将某进制数a化为十进制数b的程序框图，若输入的k=2，a=110，n=3，则输出的b=（　　）
    A．14B．12C．6D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．设p：f（x）=1+ax，在（0，2]上f（x）≥0恒成立，q函数g（x）=ax-$\frac{a}{x}$+2lnx在其定义域上存在极值．
    （1）若p为真命题，求实数a的取值范围；
    （2）如果“p∨q”为真命题，“p∧q”为假命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．把一个周长为12 cm的长方形围成一个圆柱，当圆柱的体积最大时，该圆柱的底面周长与高的比为2：1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

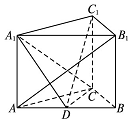    1．如图，在直三棱柱ABC-A1B1C1中，AB=4，AC=BC=3D为AB的中点，AB1⊥A1C
    （1）求点C1到平面A1CD的距离；
    （2）求二面角A1-CD-C1的平面角的余弦值．

    查看答案和解析>>

    同步练习册答案