
如图,在平面直角坐标系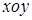 中,
中,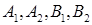 为椭圆
为椭圆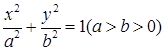 的
的
四个顶点,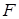 为其右焦点,直线
为其右焦点,直线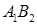 与直线
与直线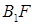 相交于点T,线段
相交于点T,线段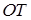 与椭圆的交点
与椭圆的交点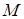 恰为线段
恰为线段 的中点,则该椭圆的离心率为__________.
的中点,则该椭圆的离心率为__________.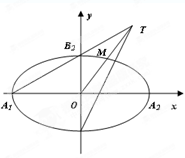
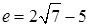
解析试题分析:对椭圆进行压缩变换,x′=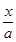 ,y′=
,y′=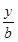 椭圆变为单位圆:x'2+y'2=1,F'(
椭圆变为单位圆:x'2+y'2=1,F'(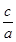 ,0)
,0)
延长TO交圆O于N,易知直线A1B1斜率为1,TM=MO=ON=1,A1B2=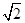 ,
,
设T(x′,y′),则TB2=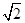 x′,y′=x′+1,由割线定理:TB2×TA1=TM×TN,
x′,y′=x′+1,由割线定理:TB2×TA1=TM×TN, 易知:B1(0,-1)直线B1T方程:
易知:B1(0,-1)直线B1T方程: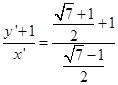 令y′=0,x′=2
令y′=0,x′=2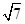 -5,即F横坐标,即原椭圆的离心率e=2
-5,即F横坐标,即原椭圆的离心率e=2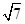 -5
-5
故答案:2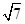 -5。
-5。
考点:本题主要考查了圆锥曲线的性质和应用,解题时要认真审题,仔细解答.
点评:解决该试题的关键是对椭圆进行压缩变换,x′=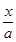 ,y′=
,y′=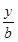 ,椭圆变为单位圆:x'2+y'2=1,F'(
,椭圆变为单位圆:x'2+y'2=1,F'(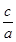 ,0).根据题设条件求出直线B1T方程,直线直线B1T与x轴交点的横坐标就是该椭圆的离心率.
,0).根据题设条件求出直线B1T方程,直线直线B1T与x轴交点的横坐标就是该椭圆的离心率.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com