
已知双曲线C: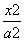 -
-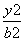 =1(a>0,b>0)的左、右焦点分别为F1、F2,离心率为3,直线y=2与C的两个交点间的距离为
=1(a>0,b>0)的左、右焦点分别为F1、F2,离心率为3,直线y=2与C的两个交点间的距离为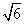 .
.
(1)求a,b;
(2)设过F2的直线l与C的左、右两支分别交于A,B两点,且|AF1|=|BF1|,证明:|AF2|,|AB|,|BF2|成等比数列.
(1)解析:由题设知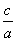 =3,即
=3,即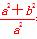 =9,故b2=8a2.
=9,故b2=8a2.
所以C的方程为8x2-y2=8a2.
将y=2代入上式,求得x=±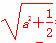 .
.
由题设知,2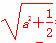 =
=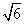 ,解得a2=1.
,解得a2=1.
所以a=1,b=2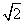 .
.
(2)证明:由(1)知,F1(-3,0),F2(3,0),C的方程为8x2-y2=8.①
由题意可设l的方程为y=k(x-3),|k|<2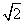 ,代入①并化简得
,代入①并化简得
(k2-8)x2-6k2x+9k2+8=0.
设A(x1,y1),B(x2,y2),则
x1≤-1,x2≥1,
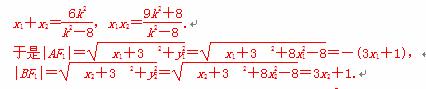 由|AF1|=|BF1|得-(3x1+1)=3x2+1,即x1+x2=-
由|AF1|=|BF1|得-(3x1+1)=3x2+1,即x1+x2=- .
.
故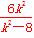 =-
=- ,解得k2=
,解得k2=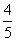 ,从而x1x2=-
,从而x1x2=-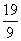 .
.
由于|AF2|=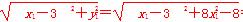 =1-3x1,
=1-3x1,
|BF2|= =
=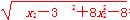 =3x2-1
=3x2-1 ,
,
故| AB|=|AF2|-|BF2|=2-3(x1+x2)=4,
AB|=|AF2|-|BF2|=2-3(x1+x2)=4,
|AF2|·|BF2|=3(x1+x2)-9x1x2-1=16.
因而|AF2|·|BF2|=|AB|2,
所以|AF2|,|AB|,|BF2|成等比数列.


科目:高中数学 来源: 题型:
在平面直角坐标系内,若曲线C:x2+y2+2ax-4ay+5a2-4=0上所有的点均在第二象限内,则实数a的取值范围为( )
A.(-∞,-2) B.(-∞,-1)
C.(1,+∞) D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知曲线C的方程是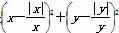 =8,给出下列三个结论:
=8,给出下列三个结论:
①曲线C与两坐标轴有公共点;
②曲线C既是中心对称图形,又是轴对称图形;
③若点P,Q在曲线C上,则|PQ|的最大值是6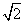 .
.
其中,所有正确结论的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com