
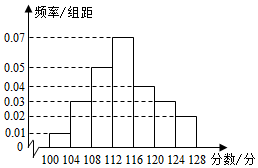
 某校高三(1)班在一次单元测试中,每位同学的考试分数都在区间[100,128]内,将该班所有同学的考试分数分为七组:[100,104),[104,108),[108,112),[112,116),[116,120),[120,124),[124,128],绘制出频率分布直方图如图所示,已知分数低于112分的有18人,则分数不低于120分的人数为( )
某校高三(1)班在一次单元测试中,每位同学的考试分数都在区间[100,128]内,将该班所有同学的考试分数分为七组:[100,104),[104,108),[108,112),[112,116),[116,120),[120,124),[124,128],绘制出频率分布直方图如图所示,已知分数低于112分的有18人,则分数不低于120分的人数为( )| A. | 10 | B. | 12 | C. | 20 | D. | 40 |
分析 由频率分布直方图求出得分数低于112分的频率,从而求出高三(1)班总人数,再求出分数不低于120分的频率,由此能求出分数不低于120分的人数.
解答 解:由频率分布直方图得分数低于112分的频率为:
(0.01+0.03+0.05)×4=0.36,
∵分数低于112分的有18人,
∴高三(1)班总人数为:n=$\frac{18}{0.36}$=50,
∵分数不低于120分的频率为:(0.03+0.02)×4=0.2,
∴分数不低于120分的人数为:50×0.2=10人.
故选:A.
点评 本题考查分数不低于120分的人数的求法,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=log2x | B. | f(x)=-x2+2x | C. | f(x)=2|x| | D. | f(x)=sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)>eaf(0) | B. | f(a)<eaf(0) | C. | f(a)<$\frac{f(0)}{{e}^{a}}$ | D. | f(a)>$\frac{f(0)}{{e}^{a}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cosx在[2kπ,2kπ+$\frac{π}{2}$](k∈Z)上是减函数 | |
| B. | y=cosx在[-π,0]上是增函数 | |
| C. | y=cosx在第一象限是减函数 | |
| D. | y=sinx和y=cosx在[$\frac{π}{2}$,π]上都是减函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com