
| A. | f(x)=log2x | B. | f(x)=-x2+2x | C. | f(x)=2|x| | D. | f(x)=sinx |
分析 根据条件分别进行验证,依次进行判断即可.
解答 解:A.f(x)=log2x为单调递增函数,不满足条件①,
B.∵f(0)=0,f(1)=-1+2=1,f($\frac{1}{2}$)=-$\frac{1}{4}+$2×$\frac{1}{2}$=$\frac{3}{4}$,
∴$\frac{1}{2}$[f(0)+f(1)]=$\frac{1}{2}$,
则f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{f({x}_{1})+f({x}_{2})}{2}$不成立,不满足条件②,
D.f(x)=sinx的图象不满足条件.比如当x1=0,x2=$\frac{π}{2}$时,f($\frac{{x}_{1}+{x}_{2}}{2}$)=f($\frac{π}{4}$)=sin$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$,
$\frac{f({x}_{1})+f({x}_{2})}{2}$=$\frac{1}{2}$(0+1)=$\frac{1}{2}$,不满足条件f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{f({x}_{1})+f({x}_{2})}{2}$.
故选:C
点评 本题主要考查抽象函数的应用,根据定义转化为进行判断或者使用排除法是解决本题的关键.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 若a∥α,a∥β,α∩β=b,则a∥b | B. | 若α⊥β,a⊥α,b⊥β则a⊥b | ||
| C. | 若α⊥β,α⊥γ,β∩γ=a,则a⊥α | D. | 若α∥β,a∥α,则a∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
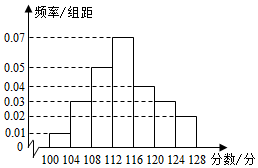 某校高三(1)班在一次单元测试中,每位同学的考试分数都在区间[100,128]内,将该班所有同学的考试分数分为七组:[100,104),[104,108),[108,112),[112,116),[116,120),[120,124),[124,128],绘制出频率分布直方图如图所示,已知分数低于112分的有18人,则分数不低于120分的人数为( )
某校高三(1)班在一次单元测试中,每位同学的考试分数都在区间[100,128]内,将该班所有同学的考试分数分为七组:[100,104),[104,108),[108,112),[112,116),[116,120),[120,124),[124,128],绘制出频率分布直方图如图所示,已知分数低于112分的有18人,则分数不低于120分的人数为( )| A. | 10 | B. | 12 | C. | 20 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com