
【题目】已知函数![]() .
.
(1)当![]() 且
且![]() 时,证明
时,证明![]() .
.
(2)令![]() ,若
,若![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
【答案】(1)见解析;(2)![]()
【解析】分析:(1)先将所证不等式转化成![]() ,再令
,再令
![]() ,求出导数,然后求出
,求出导数,然后求出![]() 的极小值,若极小值大于或等于0即证.
的极小值,若极小值大于或等于0即证.
(2)求得![]() 的导数,令
的导数,令![]() ,求出单调区间和最值,讨论
,求出单调区间和最值,讨论
①当当![]() 即
即![]() 时,
时,
②当![]() 即
即![]() 时,求出单调性,以及最小值,解不等式即可得到
时,求出单调性,以及最小值,解不等式即可得到![]() 的取值范围.
的取值范围.
详解:
(1)![]() 等价于
等价于![]() ,
,
即![]() .
.
∵![]() ,∴等价于
,∴等价于![]() .
.
令![]() ,
,
则![]() .
.
∵![]() ,∴
,∴![]() .
.
当![]() 时,
时,![]() ,
,![]() 单减;
单减;
当![]() 时,
时,![]() ,
,![]() 单增.
单增.
∴![]() 在
在![]() 处有极小值,即最小值,
处有极小值,即最小值,
∴![]() ,
,
∴![]() 且
且![]() 时,不等式
时,不等式![]() 成立.
成立.
(2)∵![]() ,∴
,∴![]() .
.
令![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单增,
上单增,
∴![]() .
.
当![]() 即
即![]() 时,
时,![]() 恒成立,即
恒成立,即![]() ,∴
,∴![]() 在
在
![]() 上单增,
上单增,
∴![]() ,所以
,所以![]() .
.
当![]() 即
即![]() 时,∵
时,∵![]() 在
在![]() 上单增,
上单增,
且![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,使
,使![]() ,即
,即![]() .
.
当![]() 时,
时,![]() ,即
,即![]() 单减;
单减;
当![]() 时,
时,![]() ,即
,即![]() 单增.
单增.
∴![]() ,
,
∴![]() ,由
,由![]() ,∴
,∴![]() ,
,
记![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上单调 递增,∴
上单调 递增,∴![]() ,∴
,∴![]() ,综上,
,综上,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以原点
为参数).在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点. 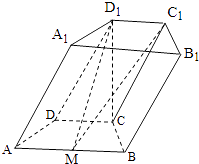
(1)求证:C1M∥平面A1ADD1;
(2)若CD1垂直于平面ABCD且CD1= ![]() ,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,部分对应值如下表,
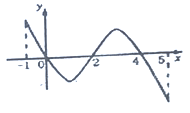
,部分对应值如下表,![]() 的导函数
的导函数![]() 的图象如图所示,给出关于
的图象如图所示,给出关于![]() 的下列命题:
的下列命题:
①函数![]() 在
在![]() 处取得极小值;
处取得极小值;
②函数![]() 在
在![]() 是减函数,在
是减函数,在![]() 是增函数;
是增函数;
③当![]() 时,函数
时,函数![]() 有4个零点;
有4个零点;
④如果当![]() 时,
时,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最小值为0.
的最小值为0.
其中所有的正确命题是__________(写出正确命题的序号).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(x+θ)+acos(x+2θ),其中a∈R,θ∈(﹣ ![]() ,
, ![]() )
)
(1)当a= ![]() ,θ=
,θ= ![]() 时,求f(x)在区间[0,π]上的最大值与最小值;
时,求f(x)在区间[0,π]上的最大值与最小值;
(2)若f( ![]() )=0,f(π)=1,求a,θ的值.
)=0,f(π)=1,求a,θ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com