
分析 令1gx=$\frac{1}{x}$,即得方程1gx-$\frac{1}{x}$=0,再令g(x)=1gx-$\frac{1}{x}$,用二分法求得交点的横坐标约为2.5.
解答 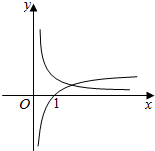 解:交点的横坐标即为方程1gx=$\frac{1}{x}$的根,由图象可知两函数只有一个交点,
解:交点的横坐标即为方程1gx=$\frac{1}{x}$的根,由图象可知两函数只有一个交点,
令f(x)=1gx-$\frac{1}{x}$.因为f(1)=-1,f(2)≈-0.2<0,f(3)≈0.14>0,
于是可知,交点在(2,3)内.
| 区间 | 中点 | f(中点) |
| (2,3) | 2.5 | -0.002 |
| (2.5,3) | 2.75 | 0.04 |
| (2.5,2.75) | 2.625 | 0.02 |
| (2.5,2.625) | 2.5625 | |
| (2.5,2.5625) |
点评 熟练掌握函数零点的判定定理及二分法求函数零点的方法、数形结合思想是解题的关键.


科目:高中数学 来源: 题型:填空题
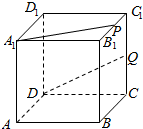 如图,在正方体ABCD-A1B1C1D1中,点P、Q分别是B1C1、CC1的中点,则直线A1P与DQ的位置关系是相交.(填“平行”、“相交”或“异面”)
如图,在正方体ABCD-A1B1C1D1中,点P、Q分别是B1C1、CC1的中点,则直线A1P与DQ的位置关系是相交.(填“平行”、“相交”或“异面”)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
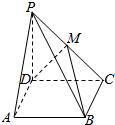 已知四棱锥P-ABCD的底面是平行四边形,如图,M是PC的中点,问向量$\overrightarrow{PA}$、$\overrightarrow{MB}$、$\overrightarrow{MD}$是否可以组成一个基底,并说明理由.
已知四棱锥P-ABCD的底面是平行四边形,如图,M是PC的中点,问向量$\overrightarrow{PA}$、$\overrightarrow{MB}$、$\overrightarrow{MD}$是否可以组成一个基底,并说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com