
���� ��1��������Բ�������ʣ�S1������з����飬���a��b���ɵó���Բ���̣�
��2����P��2$\sqrt{2}$cos����2sin�������ֱ����ֱ�߷��̣��ó�M��N�����꣬�æ���ʾ��S1��S2���Ӷ��õ��˹��ڦ��ĺ��������õ����жϴ˺����ĵ����ԣ��ó��˵���Сֵ�����Ӧ�Ħ����Ӷ��ó�P�����꣮
��� �⣺��1��˫���ߵ�������Ϊ$\sqrt{2}$������Բ��������Ϊ$\frac{\sqrt{2}}{2}$��
��$\left\{\begin{array}{l}{ab=4\sqrt{2}}\\{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{{a}^{2}-{b}^{2}={c}^{2}}\end{array}\right.$�����a=2$\sqrt{2}$��b=2��
����Բ����Ϊ$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$��
��2����P��2$\sqrt{2}$cos����2sin������0�ܦ���2���Ҧ�$��\frac{��}{2}$������$\frac{3��}{2}$����B1��0��2����B��0��-2����
��ֱ��B1P�ķ���Ϊy=$\frac{sin��-1}{\sqrt{2}cos��}$x+2��ֱ��B2P�ķ���Ϊy=$\frac{sin��+1}{\sqrt{2}cos��}$x-2��
��M��$\frac{2\sqrt{2}cos��}{sin��-1}$��4����N��$\frac{6\sqrt{2}cos��}{sin��+1}$��4����
|MN|=|$\frac{6\sqrt{2}cos��}{sin��+1}$-$\frac{2\sqrt{2}cos��}{sin��-1}$|=|$\frac{2\sqrt{2}��4-2sin����}{cos��}$|��
��S2=$\frac{1}{2}$��|MN|����4-2sin����=$\frac{4\sqrt{2}��2-sin����^{2}}{|cos��|}$����S1=$\frac{1}{2}��2b��|2\sqrt{2}cos��|$=4$\sqrt{2}$|cos��|��
���=$\frac{{S}_{2}}{{S}_{1}}$=$\frac{��2-sin����^{2}}{co{s}^{2}��}$=��$\frac{2-sin��}{cos��}$��2��
��f������=$\frac{2-sin��}{cos��}$����f�䣨����=$\frac{2sin��-1}{co{s}^{2}��}$��
��f�䣨����=0�æ�=$\frac{��}{6}$���=$\frac{5��}{6}$��
��0$������\frac{��}{6}$ʱ��f�䣨������0����$\frac{��}{6}$$������\frac{��}{2}$ʱ��f�䣨������0����$\frac{��}{2}������\frac{5��}{6}$ʱ��f�䣨������0��
��$\frac{5��}{6}������\frac{3��}{2}$ʱ��f�䣨������0����$\frac{3��}{2}������2��$ʱ��f�䣨������0��
��f��������[0��$\frac{��}{6}$]�ϵ����ݼ����ڣ�$\frac{��}{6}$��$\frac{��}{2}$���ϵ����������ڣ�$\frac{��}{2}$��$\frac{5��}{6}$]�ϵ����������ڣ�$\frac{5��}{6}$��$\frac{3��}{2}$���ϵ����ݼ����ڣ�$\frac{3��}{2}$��2�У��ϵ����ݼ���
�൱$��=\frac{��}{6}$ʱ��f������ȡ�ü�Сֵf��$\frac{��}{6}$��=$\frac{2-\frac{1}{2}}{\frac{\sqrt{3}}{2}}$=$\sqrt{3}$������=$\frac{5��}{6}$ʱ��f������ȡ�ü���ֵf��$\frac{5��}{6}$��=$\frac{2-\frac{1}{2}}{-\frac{\sqrt{3}}{2}}$=-$\sqrt{3}$��
�൱��=$\frac{��}{6}$��$\frac{5��}{6}$ʱ��|f������|ȡ����Сֵ$\sqrt{3}$��
���=f2����������СֵΪ$\sqrt{3}$��
�൱��ȡ����Сֵʱ��P������Ϊ��$\sqrt{6}$��1����-$\sqrt{6}$��1����
���� ���⿼������Բ�����ʣ�ֱ������Բ��λ�ù�ϵ�������е��⣮


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x^2}{12}-\frac{y^2}{24}=1$ | B�� | $\frac{y^2}{12}-\frac{x^2}{24}=1$ | C�� | $\frac{y^2}{24}-\frac{x^2}{12}=1$ | D�� | $\frac{x^2}{24}-\frac{y^2}{12}=1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
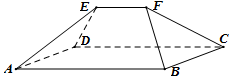 ���������������ҹ��Ŵ����ݼ�Ϊ�ḻ����ѧ�����������ᵽ��һ����Ϊ��ۻ�����������壨��ͼ������ABCDΪ���Σ���EF��AB�����˼������У�AB=4��EF=2����ADE�͡�BCF���DZ߳�Ϊ2�ĵȱ������Σ���˼�����ı����Ϊ��������
���������������ҹ��Ŵ����ݼ�Ϊ�ḻ����ѧ�����������ᵽ��һ����Ϊ��ۻ�����������壨��ͼ������ABCDΪ���Σ���EF��AB�����˼������У�AB=4��EF=2����ADE�͡�BCF���DZ߳�Ϊ2�ĵȱ������Σ���˼�����ı����Ϊ��������| A�� | $8\sqrt{3}$ | B�� | $8+8\sqrt{3}$ | C�� | $6\sqrt{2}+2\sqrt{3}$ | D�� | $8+6\sqrt{2}+2\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
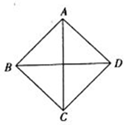 ��֪ij��������������������϶��ɣ����ü����������ͼ������ͼ�Ͳ���ͼ��Ϊ��ͼ��ʾ��ͼ�Σ������ı����DZ߳�Ϊ$\sqrt{2}$�������Σ���ü�����ı�����ǣ�������
��֪ij��������������������϶��ɣ����ü����������ͼ������ͼ�Ͳ���ͼ��Ϊ��ͼ��ʾ��ͼ�Σ������ı����DZ߳�Ϊ$\sqrt{2}$�������Σ���ü�����ı�����ǣ�������| A�� | 8$\sqrt{3}$ | B�� | 4$\sqrt{3}$ | C�� | 8$\sqrt{3}$+2 | D�� | 4$\sqrt{3}$+2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{13}{25}$ | B�� | $\frac{12}{25}$ | C�� | $\frac{13}{20}$ | D�� | $\frac{3}{5}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com