
分析 (1)确定f(x)的定义域,求导数,确定f(x)在区间[$\frac{1}{e}$,e]上的最值只可能在f(1),f($\frac{1}{e}$),f(e)取到,即可求得结论;
(2)求导函数,分类讨论,利用导数的正负,即可确定函数f(x)的单调性.
解答 解:(1)当a=-$\frac{1}{2}$时,f(x)=-$\frac{1}{2}$lnx+$\frac{1}{4}$x2+1,
∴f′(x)=$\frac{{x}^{2}-1}{2x}$,
∵f(x)的定义域为(0,+∞),
∴由f'(x)=0得x=1,
∴f(x)在区间[$\frac{1}{e}$,e]上的最值只可能在f(1),f($\frac{1}{e}$),f(e)取到,
而f(1)=$\frac{5}{4}$,f($\frac{1}{e}$)=$\frac{3}{2}$+$\frac{1}{{4e}^{2}}$,f(e)=$\frac{1}{2}$+$\frac{{e}^{2}}{4}$,
∴f(x)max=f(e)=$\frac{1}{2}$+$\frac{{e}^{2}}{4}$,f(x)min=f(1)=$\frac{5}{4}$.
(2)f′(x)=$\frac{(a+1{)x}^{2}+a}{x}$,x∈(0,+∞).
①当a+1≤0,即a≤-1时,f'(x)<0,
∴f(x)在(0,+∞)单调递减;
②当a≥0时,f'(x)>0,∴f(x)在(0,+∞)单调递增;
③当-1<a<0时,由f'(x)>0得x2>$\frac{-a}{a+1}$,
∴x>$\sqrt{\frac{-a}{a+1}}$或x<-$\sqrt{\frac{-a}{a+1}}$(舍去)
∴f(x)在($\sqrt{\frac{-a}{a+1}}$,+∞)单调递增,在(0,$\sqrt{\frac{-a}{a+1}}$)上单调递减;
综上,当a≥0时,f(x)在(0,+∞)单调递增;
当-1<a<0时,f(x)在($\sqrt{\frac{-a}{a+1}}$,+∞)单调递增,在(0,$\sqrt{\frac{-a}{a+1}}$)上单调递减;
当a≤-1时,f(x)在(0,+∞)单调递减.
点评 本题考查导数知识的运用,考查函数的单调性与最值,考查分类讨论的数学思想,正确分类是关键.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案科目:高中数学 来源: 题型:解答题
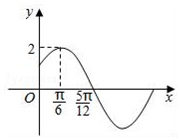 已知函数f(x)=Asin(ωx+φ)
已知函数f(x)=Asin(ωx+φ)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{9}{2}$] | B. | (-∞,1] | C. | (-∞,9] | D. | (-∞,8] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
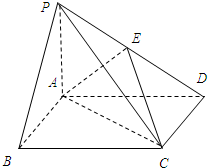 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | 10 | C. | $\frac{1}{5}$ | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com