
| A. | $\frac{1}{10}$ | B. | 10 | C. | $\frac{1}{5}$ | D. | 5 |
分析 结合调和数列的定义可得:xn+1-xn=t,(n∈N*,t为常数),从而数列{xn}是等差数列.由等差数列的性质可得x3+x18=x1+x20=20,从而20≥2$\sqrt{{x}_{3}{x}_{18}}$,由此能求出$\frac{1}{x_3}+\frac{1}{{{x_{18}}}}$的最小值.
解答 解:∵数列{an}满足$\frac{1}{{{a_{n+1}}}}-\frac{1}{a_n}=d$(n∈N*,d为常数),则称{an}为“调和数列”,
正项数列$\left\{{\frac{1}{x_n}}\right\}$为“调和数列”,
∴结合调和数列的定义可得:xn+1-xn=t,(n∈N*,t为常数),
∴数列{xn}是等差数列.
∵x1+x2+x3+…+x20=200,
∴结合等差数列的性质可得:x1+x2+x3+…+x20=10(x1+x20)=200,
∴x3+x18=x1+x20=20,
∴20≥2$\sqrt{{x}_{3}{x}_{18}}$,即x3x18≤100.
∴$\frac{1}{x_3}+\frac{1}{{{x_{18}}}}$=$\frac{{x}_{3}+{x}_{18}}{{x}_{3}{x}_{18}}$=$\frac{20}{{x}_{3}{x}_{18}}$≥$\frac{20}{100}$=$\frac{1}{5}$,
当且仅当x3=x18=10时,取等号,
∴$\frac{1}{x_3}+\frac{1}{{{x_{18}}}}$的最小值为$\frac{1}{5}$.
故选:C.
点评 本题考查数列中两项和的最小值的求法,涉及到等差数列、等比数列、基本不等式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
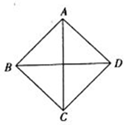 已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )
已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )| A. | 8$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$+2 | D. | 4$\sqrt{3}$+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{25}$ | B. | $\frac{12}{25}$ | C. | $\frac{13}{20}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com