练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．（3x-2）5（1-x+x2）展开式中x3的系数为2040．

    分析 利用二项式定理展开：（3x-2）5进而得出．

    解答 解：（3x-2）5=（3x）5-2${∁}_{5}^{1}（3x）^{4}$+${2}^{2}{∁}_{5}^{2}（3x）^{3}$-23${∁}_{5}^{3}（3x）^{2}$+${2}^{4}{∁}_{5}^{4}$•3x-25．
    ∴（3x-2）5（1-x+x2）展开式中x3的系数=${2}^{2}{∁}_{5}^{2}×{3}^{3}$$-{2}^{3}{∁}_{5}^{3}×{3}^{2}$×（-1）+${2}^{4}{∁}_{5}^{4}$•3=2040．
    故答案为：2040．

    点评 本题考查了二项式定理的应用，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    6．若数列{an}满足$\frac{1}{{{a_{n+1}}}}-\frac{1}{a_n}=d$（n∈N*，d为常数），则称{an}为“调和数列”，已知正项数列$\left\{{\frac{1}{x_n}}\right\}$为“调和数列”，且x1+x2+…+x20=200，则$\frac{1}{x_3}+\frac{1}{{{x_{18}}}}$的最小值为（　　）
    A．$\frac{1}{10}$B．10C．$\frac{1}{5}$D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．如图为某市2017年2月28天的日空气质量指数折线图．

    由中国空气质量在线监测分析平台提供的空气质量指数标准如下：
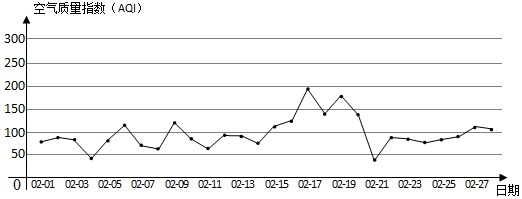
    空气质量指数（0，50]（50，100]（100，150]（150，200]（200，300]300以上
    空气质量等级1级优2级良3级轻度污染4级中度污染5级重度污染6级严重污染
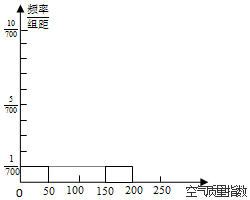
    （Ⅰ）请根据所给的折线图补全下方的频率分布直方图（并用铅笔涂黑矩形区域），并估算该市2月份空气质量指数监测数据的平均数（保留小数点后一位）；

    （Ⅱ）研究人员发现，空气质量指数测评中PM2.5与燃烧排放的CO两个项目存在线性相关关系，以100ug/m3为单位，如表给出PM2.5与CO的相关数据：
    CO（x）0.511.5
    PM2.5（y）124
    求y关于x的回归方程，并估计当CO排放量是200ug/m3时，PM2.5的值．
    （用最小二乘法求回归方程的系数是$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n•\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n•{{\overline x}^2}}}}$$，\hat a=\overline y-\hat b\overline x$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知点A（3，0），$\overrightarrow{EA}$=（2，1），$\overrightarrow{EF}$=（1，2），若P（2，0）满足$\overrightarrow{EP}$=λ$\overrightarrow{EA}$+μ$\overrightarrow{EF}$，则λ+μ=$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．复数$\frac{（1+i）^{2}}{2i}$=（　　）
    A．1B．-1C．iD．-i

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．设数列{an}的前n项和为Sn，满足Sn=（2n+1）an-（2n-1）•2n-1-1
    （1）求a1，a2，a3的值；
    （2）求数列{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知sinθ=$\frac{3}{5}$，θ为第二象限角，则cos2θ=$\frac{7}{25}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．某少数民族的刺绣有着悠久的历史，图中（1）、（2）、（3）、（4）为她们刺锈最简单的四个图案，这些图案都是由小正方向构成，小正方形数越多刺锈越漂亮，向按同样的规律刺锈（小正方形的摆放规律相同），设第n个图形包含f（n）个小正方形

    （1）求f（6）的值
    （2）求出f（n）的表达式
    （3）求证：当n≥2时，$\frac{1}{f（1）}$+$\frac{1}{f（2）-1}$+$\frac{1}{f（3）-1}$+…+$\frac{1}{f（n）-1}$＜$\frac{3}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设p：实数x满足x2-4ax+3a2＜0，其中a≠0，命题q：实数x满足$\left\{\begin{array}{l}{{x}^{2}-x-6≤0}\\{{x}^{2}+2x-8＞0}\end{array}\right.$，
    （1）若a=1，且p∧q为真，求实数x的取值范围；
    （2）若p是q的必要不充分条件，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案