
分析 (1)由二次函数f(x)=ax2-4x+c的值域,推出ac=4,判断f(-1)≠f(1),f(-1)≠-f(1),得到此函数是非奇非偶函数.
(2)求出函数的单调递增区间.设x1、x2是满足${x_2}>{x_1}≥\frac{2}{a}$的任意两个数,列出不等式,推出f(x2)>f(x1),即可判断函数是单调递增.
(3)f(x)=ax2-4x+c,当${x_0}=\frac{2}{a}≥1$,即0<a≤2时,当${x_0}=\frac{2}{a}<1$,即a>2时求出最小值即可.
解答 (16分)解:(1)由二次函数f(x)=ax2-4x+c的值域为[0,+∞),得a>0且$\frac{4ac-16}{4a}=0$,
解得ac=4.…(2分)
∵f(1)=a+c-4,f(-1)=a+c+4,a>0且c>0,从而f(-1)≠f(1),f(-1)≠-f(1),
∴此函数是非奇非偶函数.…(6分)
(2)函数的单调递增区间是[$\frac{2}{a}$,+∞).设x1、x2是满足${x_2}>{x_1}≥\frac{2}{a}$的任意两个数,从而有${x_2}-\frac{2}{a}>{x_1}-\frac{2}{a}≥0$,∴${({x_2}-\frac{2}{a})^2}>{({x_1}-\frac{2}{a})^2}$.又a>0,∴$a{({x_2}-\frac{2}{a})^2}>a{({x_1}-\frac{2}{a})^2}$,
从而$a{({x_2}-\frac{2}{a})^2}+c-\frac{4}{a}>a{({x_1}-\frac{2}{a})^2}+c-\frac{4}{a}$,
即$ax_2^2-4{x_2}+c>ax_1^2-4{x_1}+c$,从而f(x2)>f(x1),∴函数在[$\frac{2}{a}$,+∞)上是单调递增.…(10分)
(3)f(x)=ax2-4x+c,又a>0,${x_0}=\frac{2}{a}$,x∈[1,+∞)
当${x_0}=\frac{2}{a}≥1$,即0<a≤2时,最小值g(a)=f(x0)=0
当${x_0}=\frac{2}{a}<1$,即a>2时,最小值$g(a)=f(1)=a+c-4=a+\frac{4}{a}-4$
综上,最小值$g(a)=\left\{{\begin{array}{l}0&{0<a≤2}\\{a+\frac{4}{a}-4}&{a>2}\end{array}}\right.$…(14分)
当0<a≤2时,最小值g(a)=0
当a>2时,最小值$g(a)=a+\frac{4}{a}-4∈(0,+∞)$
综上y=g(a)的值域为[0,+∞)…(16分)
点评 本题考查二次函数的简单性质的应用,函数的单调性以及二次函数的对称轴的关系,函数的最值的求法,考查计算能力.


科目:高中数学 来源: 题型:解答题
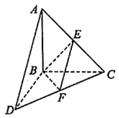 如图,三棱锥A-BCD中,△ABC和△BCD所在平面互相垂直,且AB=CD=4,AC=4$\sqrt{2}$,CD=4$\sqrt{3}$,∠ACB=45°,E,F分别为MN的中点.
如图,三棱锥A-BCD中,△ABC和△BCD所在平面互相垂直,且AB=CD=4,AC=4$\sqrt{2}$,CD=4$\sqrt{3}$,∠ACB=45°,E,F分别为MN的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $0<a≤\frac{π}{2}$ | B. | $0<a≤\frac{π}{12}$ | ||
| C. | $a=kπ+\frac{π}{12},k∈{N^*}$ | D. | $2kπ<a≤2kπ+\frac{π}{12},k∈N$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 336种 | B. | 320种 | C. | 192种 | D. | 144种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②③ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com