Question

8．在△ABC中，若对任意的m∈R，|$\overrightarrow{CA}$-m$\overrightarrow{CB}$|≥|$\overrightarrow{AB}$|恒成立，则△ABC的形状为（　　）

• A． 直角三角形
• B． 锐角三角形
• C． 钝角三角形
• D． 不确定

Answer 1

分析 能够分析出$|\overrightarrow{CA}-m\overrightarrow{CB}|$$≥|\overrightarrow{AB}|$表示直线BC上的点到点A的最短距离为向量$\overrightarrow{AB}$的长度，从而得到AB应与BC垂直，从而便得出了△ABC的形状．

解答 解：向量m$\overrightarrow{CB}$的终点在直线BC上，如图，$\overrightarrow{CA}-m\overrightarrow{CB}$表示起点是直线BC上一点，而指向A点的向量，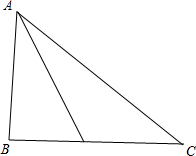
∴$|\overrightarrow{CA}-m\overrightarrow{CB}|$表示直线BC上的一点到点A的距离，该距离最小值为$|\overrightarrow{AB}|$；
∴AB⊥BC；
∴△ABC为直角三角形．
故选A．

点评 考查向量数乘、减法的几何意义，向量长度的概念，清楚直线外一点到直线上哪点的距离最短．