
 题:(本小题10分,实验班同学必做,其他班学生选做)
题:(本小题10分,实验班同学必做,其他班学生选做) -
-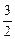 在闭区间
在闭区间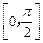 上的最大值为1?若存在,求出对应的a值;若不存在,说明理由.
上的最大值为1?若存在,求出对应的a值;若不存在,说明理由.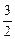 使得f (x)在闭区间
使得f (x)在闭区间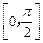 上的最大值为1
上的最大值为1 -
-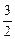
 -
-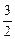 =-cos2x+acosx+
=-cos2x+acosx+ -
-
 a)2+
a)2+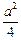 +
+ -
-
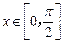 ,∴0≤cos
,∴0≤cos x≤1, ………………1分
x≤1, ………………1分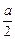 >1,即a>2,则当cosx=1时,f (x)取得最大值,
>1,即a>2,则当cosx=1时,f (x)取得最大值, a)2+
a)2+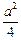 +
+ -
- =
=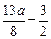 ……………3分
……………3分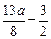 =1,解得
=1,解得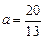 <2(舍去) ……………4分
<2(舍去) ……………4分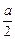 ≤1,即0≤a≤2,则当cosx=
≤1,即0≤a≤2,则当cosx=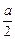 时,f (x)取得最大值,
时,f (x)取得最大值, a-
a- a)2+
a)2+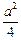 +
+ -
- =
=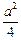 +
+ -
- ……………6分
……………6分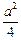 +
+ -
- =1,解得
=1,解得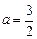 或
或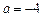 <0(舍去) ……………7分
<0(舍去) ……………7分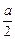 <0,即a<0,则当cosx=0时,f (x)取得最大值,
<0,即a<0,则当cosx=0时,f (x)取得最大值, a)2+
a)2+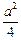 +
+ -
- =
= -
- ……………8分
……………8分 -
- =1
=1 ,解得
,解得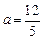 >0(舍去) ……………9分
>0(舍去) ……………9分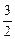 使得f (x)在闭区间
使得f (x)在闭区间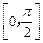 上的最大值为1 ……………10分
上的最大值为1 ……………10分

科目:高中数学 来源:不详 题型:单选题
 是
是 A.最小正周期为 且在[ 且在[ ]内有且只有三个零点的函数; ]内有且只有三个零点的函数; |
B.最小正周期为 且在[ 且在[ ]内有且只有二个零点的函数; ]内有且只有二个零点的函数; |
C.最小正周期为 且在[ 且在[ ]内有且只有三个零点的函数; ]内有且只有三个零点的函数; |
D.最小正周期为 且在[ 且在[ ]内有且只有二个零点的函数. ]内有且只有二个零点的函数. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
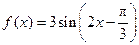 的图象为
的图象为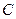 ,则如下结论中正确的序号是 _____
,则如下结论中正确的序号是 _____  关于直线
关于直线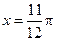 对称;
对称; 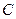 关于点
关于点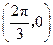 对称;
对称; 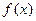 在区间
在区间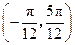 内是增函数;
内是增函数; 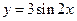 的图角向右平移
的图角向右平移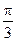 个单位长
个单位长 度可以得到图象
度可以得到图象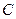 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com