Question

5．O-xyz坐标系内xoy平面内0≤y≤2-x²绕y轴旋转一周构成一个不透光立体，在（1，0，1）设置一光源，在xoy平面内有一以原点为圆心C被光照到的长度为2π，则曲线C上未被照到的长度为2π（r-1）．

Answer 1

分析 根据题意所研究的是过光源点的抛物面的切面在xoy平面中与圆的交线所构成平面几何图形的问题．

解答 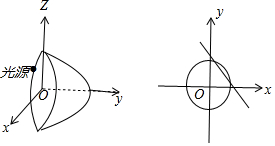解：如图所示；
由x²+z²=2-y知，
抛物面y=2-x²-z²，y对x求偏导数得$\frac{αy}{αx}$=-2x，
得l₁：$\left\{\begin{array}{l}{y=-2x+2}\\{z=1}\end{array}\right.$；
y对z求偏导数得$\frac{αy}{αz}$=-2z，得l₂：$\left\{\begin{array}{l}{y=-2z+2}\\{x=1}\end{array}\right.$；
取（0，2，1），（1，2，0），（1，0，1），
设切面ax+by+cz+d=0，
则$\left\{\begin{array}{l}{2b+c+d=0}\\{a+2b+d=0}\\{a+c+d=0}\end{array}\right.$，
得切面2x+y+2z-4=0，
故交线为2x+y-4=0；
由d=$\frac{4\sqrt{5}}{5}$，得$\left\{\begin{array}{l}{cosθ=\frac{d}{r}}\\{2θ•r=2π}\end{array}\right.$，可解得r的值；
所以l=2π（r-1）．
故答案为：l=2π（r-1）．

点评 本题是北大2008自主招生最难的一道数学试题，解题时要有很高的想象力、推理能力，也需要高超的解题技巧得到切面与交线，需要高等数学中偏导数知识，是难题．