
分析 (1)利用三种方程的转化方程,即可写出曲线C的直角坐标方程和直线l的参数方程;
(2)将参数方程代入曲线C的直角坐标方程,及参数的几何意义,即可得到$\frac{1}{|PA|}+\frac{1}{|PB|}$的值.
解答 解:(1)曲线C的极坐标方程化为直角坐标方程为x2+y2-2x-4y=0,
化为标准方程为:(x-1)2+(y-2)2=5,P$(3,\frac{π}{2})$化为直角坐标为P(0,3),
直线l的参数方程为$\left\{{\begin{array}{l}{x=tcos\frac{π}{3}}\\{y=3+tsin\frac{π}{3}}\end{array}}\right.$即$\left\{{\begin{array}{l}{x=\frac{1}{2}t}\\{y=3+\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$(t为参数).…(5分)
(2)将l的参数方程代入曲线C的直角坐标方程,得${(\frac{1}{2}t-1)^2}+{(\frac{{\sqrt{3}}}{2}t+1)^2}=5$,
整理得:${t^2}+(\sqrt{3}-1)t-3=0$,
显然有△>0,则t1+t2=-$\sqrt{3}$+1,t1t2=-3,
|PA|+|PB|=$\sqrt{16-2\sqrt{3}}$,
所以$\frac{1}{|PA|}+\frac{1}{|PB|}$=$\frac{\sqrt{16-2\sqrt{3}}}{3}$.…(10分)
点评 本题考查直线的参数方程和应用,考查韦达定理和运用,考查基本的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 3 | C. | $6\sqrt{2}$ | D. | $3\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组号 | 分组 | 频数 |
| 1 | [0.5,1) | 20 |
| 2 | [1,1.5) | 40 |
| 3 | [1.5,2) | 80 |
| 4 | [2,2.5) | 120 |
| 5 | [2.5,3) | 60 |
| 6 | [3,3.5) | 40 |
| 7 | [3.5,4) | 20 |
| 8 | [4,4.5) | 20 |
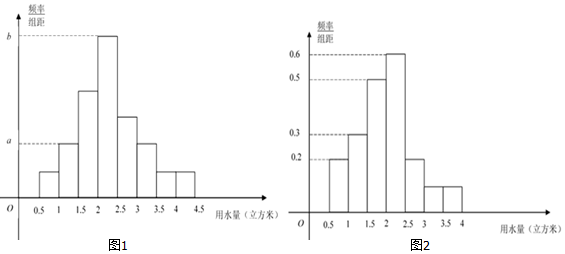
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨q | B. | p∧q | C. | (¬p)∨(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com