
| 组号 | 分组 | 频数 |
| 1 | [0.5,1) | 20 |
| 2 | [1,1.5) | 40 |
| 3 | [1.5,2) | 80 |
| 4 | [2,2.5) | 120 |
| 5 | [2.5,3) | 60 |
| 6 | [3,3.5) | 40 |
| 7 | [3.5,4) | 20 |
| 8 | [4,4.5) | 20 |
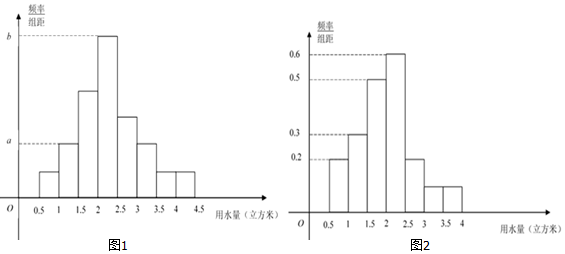
分析 (Ⅰ)由数据分组及频数分布表能求出a,b的值.
(Ⅱ)设这名住户一个月用水量小于3立方米为事件A,利用等可能事件概率计算公式能求出这名住户一个月用水量小于3立方米的概率.
(Ⅲ)由图可知小区人均月用水量低于2.5立方米,则称为“节水小区”,由图求出三个月后的该小区人均用水量,由此得到三个月后,估计小区能达到“节水小区”的标准.
解答 解:(Ⅰ)由数据分组及频数分布表知:
a=$\frac{\frac{40}{400}}{0.5}$=0.2,b=$\frac{\frac{120}{40}}{0.5}$=0.6.
(Ⅱ)设这名住户一个月用水量小于3立方米为事件A,
则这名住户一个月用水量小于3立方米的概率P(A)=$\frac{20+40+80+120+60}{400}$=0.8.
(Ⅲ)∵该小区居民月用水量低于这一标准的比例为30%,
∴由图可知小区人均月用水量低于2.5立方米,则称为“节水小区”,
由图可知,三个月后的该小区人均用水量为:
1×0.1+1.5×0.15+2×0.25+2.5×0.3+3×0.1+3.5×0.05+4×0.05=2.25<2.5,
∴三个月后,估计小区能达到“节水小区”的标准.
点评 本题考查频率分布直方图的应用,考查概率的求法,考查平均数的求法及应用,考查推理论证能力、运算求解能力,考查数形结合思想、转化化归思想,是中档题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题

| A. | 3$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,AP⊥BP,AC⊥BC,∠PAB=60°,∠ABC=45°,D是AB中点,E,F分别为PD,PC的中点.
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,AP⊥BP,AC⊥BC,∠PAB=60°,∠ABC=45°,D是AB中点,E,F分别为PD,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 乙,丁 | B. | 甲,丙 | C. | 甲,丁 | D. | 乙,丙 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
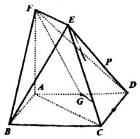 如图,正方形ABCD和梯形ACEF所在的平面相互垂直,EF∥AC,AF⊥AC,G为AD的中点,$AB=AF=2,EF=\sqrt{2}$.
如图,正方形ABCD和梯形ACEF所在的平面相互垂直,EF∥AC,AF⊥AC,G为AD的中点,$AB=AF=2,EF=\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com