
分析 将a2+b+3=ab化为(2a-2)(b-a-1)=8,再利用基本不等式,求解不等式即可求得a+b的取值范围,从而得到a+b的最小值.
解答 解:由a2+b+3=ab得a2-2a+1-b(a-1)+2(a-1)=-4,
即(a-1)2-b(a-1)+2(a-1)=-4,
∴(a-1)(a-1-b+2)=-4
∴(2a-2)(b-a-1)=8,
∴8=(2a-2)(b-a-1)≤$(\frac{2a-2+b-a+1}{2})^{2}$=$(\frac{a+b-3}{2})^{2}$
解得a+b≥3+4$\sqrt{2}$,取等号的条件是2a-2=b-a-1且(2a-2)(b-a-1)=8,解得a=$\sqrt{2}$-1,b=3$\sqrt{2}$,
∴a+b的最小值为3+4$\sqrt{2}$.
故答案为:3+4$\sqrt{2}$.
点评 本题考查了基本不等式在最值问题中的应用.在应用基本不等式求最值时要注意“一正、二定、三相等”的判断.运用基本不等式解题的关键是寻找和为定值或者是积为定值,难点在于如何合理正确的构造出定值.属于中档题


科目:高中数学 来源: 题型:选择题
| A. | (-1,9) | B. | (-9,1) | C. | (-∞,-1)∪(9,+∞) | D. | (-∞,-9)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
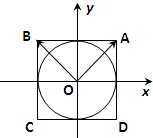 如图,在平面直角坐标系xoy中,圆x2+y2=r2(r>0)内切于正方形ABCD,任取圆上一点P,若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则$\frac{1}{4}$是m2,n2的等差中项,现有一椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)内切于矩形ABCD,任取椭圆上一点P,若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m2,n2的等差中项为( )
如图,在平面直角坐标系xoy中,圆x2+y2=r2(r>0)内切于正方形ABCD,任取圆上一点P,若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则$\frac{1}{4}$是m2,n2的等差中项,现有一椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)内切于矩形ABCD,任取椭圆上一点P,若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m2,n2的等差中项为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x}{2}$-3<$\frac{x}{3}$-3 | B. | $\left\{\begin{array}{l}{x-2<0}\\{2-3x>1}\end{array}\right.$ | C. | x2-2x>0 | D. | |x-1|<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
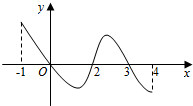 已知函数f(x)的定义域为[-1,4],部分对应值如表,
已知函数f(x)的定义域为[-1,4],部分对应值如表,| x | -1 | 0 | 2 | 3 | 4 |
| f(x) | 1 | 2 | 0 | 2 | 0 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com