
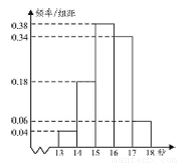
高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
(1)若成绩大于等于14秒且小于16秒规定为良好,求该班在这次百米测试中成绩为良好的人数.
(2)请根据频率分布直方图,估计样本数据的众数和中位数(精确到0.01).
(3)设 表示该班两个学生的百米测试成绩,已知
表示该班两个学生的百米测试成绩,已知 ,求事件
,求事件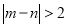 的概率.
的概率.
(1)28人;(2)众数为15.5,中位数15.74;(3)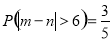 .
.
【解析】
试题分析:(1)解决频率分布直方图的问题,关键在于找出图中数据之间的关系,这些数据中,比较明显的有组距、 ,间接的有频率,小长方形的面积,合理使用这些数据,再结合两个等量关系:小长方形的面积等于频率,小长方形的面积之和等于1,因此频率之和为1;(2)最高矩形的底边的中点的横坐标即是众数,中位数左边和右边的小长方形的面积和相等的;(3)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举.
,间接的有频率,小长方形的面积,合理使用这些数据,再结合两个等量关系:小长方形的面积等于频率,小长方形的面积之和等于1,因此频率之和为1;(2)最高矩形的底边的中点的横坐标即是众数,中位数左边和右边的小长方形的面积和相等的;(3)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举.
试题解析:解(1)根据直方图可知成绩在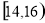 内的人数:
内的人数: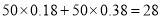 人
人
由图可知众数落在第三组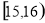 是
是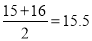
因为数据落在第一、二组的频率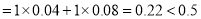
数据落在第一、二、三组的频率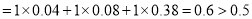
所以中位数一定落在第三组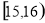 中.
中.
假设中位数是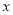 ,所以
,所以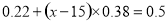
解得中位数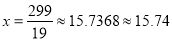
成绩在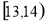 的人数有:
的人数有: 人,设为
人,设为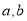
成绩在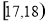 的人数有:
的人数有: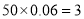 人,设为
人,设为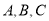
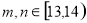 时有
时有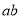 一种情况,
一种情况,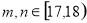 时有
时有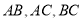 三种情况
三种情况
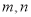 分布在
分布在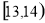 和
和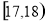 时有
时有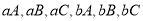 六种情况,基本事件的总数为10
六种情况,基本事件的总数为10
事件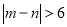 由6个基本事件组成.
由6个基本事件组成.
所以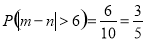 .
.
考点:(1)频率分布直方图的认识;(2)求随机事件的概率.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016届广东省清远市高一下学期期末考试数学试卷(解析版) 题型:填空题
某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本,若样本中的青年职工为7人,则样本容量为 _________ 人.
查看答案和解析>>
科目:高中数学 来源:2016届广东省清远市高一下学期期末考试数学试卷(解析版) 题型:选择题
为了从甲乙两人中选一人参加数学竞赛,老师将二人最近6次数学测试的分数进行统计,甲乙两人的平均成绩分别是 、
、 ,则下列说法正确的是( )
,则下列说法正确的是( )
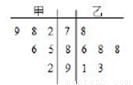
A.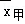 >
> ,乙比甲成绩稳定,应选乙参加比赛
,乙比甲成绩稳定,应选乙参加比赛
B.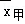 >
> ,甲比乙成绩稳定,应选甲参加比赛
,甲比乙成绩稳定,应选甲参加比赛
C.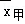 <
< ,甲比乙成绩稳定,应选甲参加比赛
,甲比乙成绩稳定,应选甲参加比赛
D.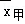 <
< ,乙比甲成绩稳定,应选乙参加比赛
,乙比甲成绩稳定,应选乙参加比赛
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com