
| A�� | $|{\overrightarrow a}|=|{\overrightarrow b}|$ | B�� | $\overrightarrow a��\overrightarrow b$ | C�� | $��\overrightarrow a-\overrightarrow b����\overrightarrow a$ | D�� | $\overrightarrow a•\overrightarrow b=8$ |
���� ��$\overrightarrow a$=��0��4����$\overrightarrow b$=��2��2��֪|$\overrightarrow a$|=4��|$\overrightarrow b$|=2$\sqrt{2}$����$\overrightarrow{a}$•$\overrightarrow b$=0•2+4•2=8���Ӷ�ȷ���𰸣�
��� �⣺��$\overrightarrow a$=��0��4����$\overrightarrow b$=��2��2����
��|$\overrightarrow a$|=4��|$\overrightarrow b$|=2$\sqrt{2}$��
$\overrightarrow{a}$•$\overrightarrow b$=0•2+4•2=8��
��ѡ��D��
���� ���⿼����ƽ�������������������㣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ˡ�2 | B�� | �ˣ�3 | C�� | �ˡ�3 | D�� | �ˣ�2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
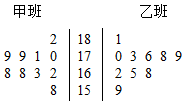 ��ij��ѧ�ļ����������и������ȡ10��ͬѧ���ֱ�������ǵ����ߣ���λ��cm�����õ��������ݵľ�Ҷͼ��ͼ��ʾ�������Ұ౻��ȡ����10��ͬѧ���������ȡ2�����߲�����173cm��ͬѧ��������Ϊ176cm��ͬѧ���鵽�ĸ���Ϊ$\frac{2}{5}$��
��ij��ѧ�ļ����������и������ȡ10��ͬѧ���ֱ�������ǵ����ߣ���λ��cm�����õ��������ݵľ�Ҷͼ��ͼ��ʾ�������Ұ౻��ȡ����10��ͬѧ���������ȡ2�����߲�����173cm��ͬѧ��������Ϊ176cm��ͬѧ���鵽�ĸ���Ϊ$\frac{2}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
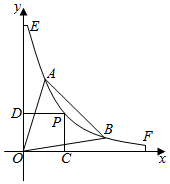 ���õ��������������ֱ���뻡�����ϣ�ǰ�����û��ߣ�����ֱ���ͣ��ֽ�����������ǽ�ߣ���ǽ�潨����ͼ��ʾ��ֱ������ϵ������EF�ķ���Ϊy=$\frac{60}{x}$��5��x��12�������̳�������ֱ��x+y-16=0�뻡�߽���A��B���㣮���ڻ���EF��ѡȡһ��P�ֱ���x�ᡢy��Ĵ��ߣ�����ΪC��D���ı���OCPD��OΪ����ԭ�㣩��������OAB�Ĺ��������ڷ��õ��ԣ����P������Ϊ��x��y���������������ΪS������λ�����ף�
���õ��������������ֱ���뻡�����ϣ�ǰ�����û��ߣ�����ֱ���ͣ��ֽ�����������ǽ�ߣ���ǽ�潨����ͼ��ʾ��ֱ������ϵ������EF�ķ���Ϊy=$\frac{60}{x}$��5��x��12�������̳�������ֱ��x+y-16=0�뻡�߽���A��B���㣮���ڻ���EF��ѡȡһ��P�ֱ���x�ᡢy��Ĵ��ߣ�����ΪC��D���ı���OCPD��OΪ����ԭ�㣩��������OAB�Ĺ��������ڷ��õ��ԣ����P������Ϊ��x��y���������������ΪS������λ�����ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a�ͦ���a��b����b�Φ� | B�� | ��a�Φ���a��b����b�ͦ� | C�� | ��a�ͦ���b⊆������a��b | D�� | ��a�Φ���b�Φ�����a��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com