
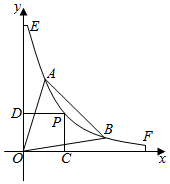
 家用电脑桌的桌面采用直线与弧线相结合,前部采用弧线,后部改用直线型.现将电脑桌靠在墙边,沿墙面建立如图所示的直角坐标系.弧线EF的方程为y=$\frac{60}{x}$(5≤x≤12).键盘抽屉所在直线x+y-16=0与弧线交于A,B两点.拟在弧线EF上选取一点P分别作x轴、y轴的垂线.垂足为C,D.四边形OCPD(O为坐标原点)与三角形OAB的公共区域内放置电脑.设点P的坐标为(x,y).公共部分面积为S.(单位:分米)
家用电脑桌的桌面采用直线与弧线相结合,前部采用弧线,后部改用直线型.现将电脑桌靠在墙边,沿墙面建立如图所示的直角坐标系.弧线EF的方程为y=$\frac{60}{x}$(5≤x≤12).键盘抽屉所在直线x+y-16=0与弧线交于A,B两点.拟在弧线EF上选取一点P分别作x轴、y轴的垂线.垂足为C,D.四边形OCPD(O为坐标原点)与三角形OAB的公共区域内放置电脑.设点P的坐标为(x,y).公共部分面积为S.(单位:分米)分析 (1)由题意可知,A(6,10),B(10,6),分段讨论即可求出相应的解析式;
(2)根据函数的单调性和基本不等式即可求出最值.
解答 解:(1)由题意可知,$\left\{\begin{array}{l}{y=\frac{60}{x}}\\{x+y-16=0}\end{array}\right.$解得$\left\{\begin{array}{l}{x=6}\\{y=10}\end{array}\right.$或$\left\{\begin{array}{l}{x=10}\\{y=6}\end{array}\right.$,
即A(6,10),B(10,6),
当5≤x≤6时,S=$\frac{8{x}^{2}}{15}$,
当6<x<10时,S=60-$\frac{3}{10}$(x2+$\frac{3600}{{x}^{2}}$),
当10≤x≤12时,S=$\frac{1920}{{x}^{2}}$,
故S=$\left\{\begin{array}{l}{\frac{8}{15}{x}^{2},5≤x≤6}\\{60-\frac{3}{10}({x}^{2}+\frac{3600}{{x}^{2}}),6<x<10}\\{\frac{1920}{{x}^{2}},10≤x≤12}\end{array}\right.$;
(2)当当5≤x≤6时,S=$\frac{8{x}^{2}}{15}$为单调递增函数,S≤$\frac{96}{5}$,
当6<x<10时,S=60-$\frac{3}{10}$(x2+$\frac{3600}{{x}^{2}}$)≤60-$\frac{3}{5}$$\sqrt{{x}^{2}+\frac{3600}{{x}^{2}}}$=24,当且仅当x=2$\sqrt{15}$时取等号
当10≤x≤12时,S=$\frac{1920}{{x}^{2}}$为单调递减函数,S≤$\frac{96}{5}$,
综上,S的最大值为24平方分米,此时x=2$\sqrt{15}$分米.
点评 本题考查函数在实际生活中的应用,考查了数学的建模能力,空间想象能力,数学阅读能力和解决实际问题的能力,属于中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $|{\overrightarrow a}|=|{\overrightarrow b}|$ | B. | $\overrightarrow a⊥\overrightarrow b$ | C. | $(\overrightarrow a-\overrightarrow b)∥\overrightarrow a$ | D. | $\overrightarrow a•\overrightarrow b=8$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{2}$ | C. | -$\frac{π}{6}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com