
分析 利用数量的数量积将不等式组进行化简,设M(s,t),将条件进行中转化,即可得到结论.
解答 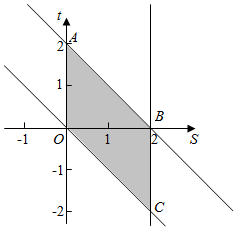 解:由$\left\{\begin{array}{l}0≤\overrightarrow{OM}•\;\overrightarrow{OA}≤1\\ 0≤\overrightarrow{OM}•\;\overrightarrow{OB}≤2\end{array}\right.$,得$\left\{\begin{array}{l}0≤x+y≤2\\ 0≤x≤1\end{array}\right.$
解:由$\left\{\begin{array}{l}0≤\overrightarrow{OM}•\;\overrightarrow{OA}≤1\\ 0≤\overrightarrow{OM}•\;\overrightarrow{OB}≤2\end{array}\right.$,得$\left\{\begin{array}{l}0≤x+y≤2\\ 0≤x≤1\end{array}\right.$
设M(s,t),则$\left\{\begin{array}{l}s=x+y\\ t=x-y\end{array}\right.$,解得$\left\{\begin{array}{l}x=\frac{1}{2}(s+t)\\ y=\frac{1}{2}(s-t)\end{array}\right.$,
由$\left\{\begin{array}{l}0≤x+y≤2\\ 0≤x≤1\end{array}\right.$,得$\left\{\begin{array}{l}0≤s+t≤2\\ 0≤s≤2\end{array}\right.$.
作出不等式组对应的平面区域,
则对应平行四边形OABC,
则A(0,2),B(2,0),C(2,-2),
则四边形的面积S=2×$\frac{1}{2}×2×2=4$,
故答案为:4.
点评 本题主要考查二元一次不等式组表示平面区域,利用向量的数量积将不等式进行转化是解决本题的关键.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1-\sqrt{2},\sqrt{2}]$ | B. | $[1-\sqrt{2},\sqrt{2}]$ | C. | $[\frac{1}{2},\sqrt{2}]$ | D. | $(\frac{1}{2},\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
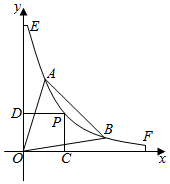 家用电脑桌的桌面采用直线与弧线相结合,前部采用弧线,后部改用直线型.现将电脑桌靠在墙边,沿墙面建立如图所示的直角坐标系.弧线EF的方程为y=$\frac{60}{x}$(5≤x≤12).键盘抽屉所在直线x+y-16=0与弧线交于A,B两点.拟在弧线EF上选取一点P分别作x轴、y轴的垂线.垂足为C,D.四边形OCPD(O为坐标原点)与三角形OAB的公共区域内放置电脑.设点P的坐标为(x,y).公共部分面积为S.(单位:分米)
家用电脑桌的桌面采用直线与弧线相结合,前部采用弧线,后部改用直线型.现将电脑桌靠在墙边,沿墙面建立如图所示的直角坐标系.弧线EF的方程为y=$\frac{60}{x}$(5≤x≤12).键盘抽屉所在直线x+y-16=0与弧线交于A,B两点.拟在弧线EF上选取一点P分别作x轴、y轴的垂线.垂足为C,D.四边形OCPD(O为坐标原点)与三角形OAB的公共区域内放置电脑.设点P的坐标为(x,y).公共部分面积为S.(单位:分米)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com