
| A. | $(1-\sqrt{2},\sqrt{2}]$ | B. | $[1-\sqrt{2},\sqrt{2}]$ | C. | $[\frac{1}{2},\sqrt{2}]$ | D. | $(\frac{1}{2},\sqrt{2}]$ |
分析 根据函数奇偶性的定义先求出a的值,根据函数奇偶性和单调性的性质将不等式进行转化进行求解即可.
解答 解:因为函数f(x)在定义域[2-a,3]上是偶函数,所以2-a+3=0,所以a=5.
所以$f(-{m^2}-\frac{a}{5})>f(-{m^2}+2m-2)$,即f(-m2-1)>f(-m2+2m-2),
所以函数f(x)在[-3,0]上单调递减,而-m2-1<0,-m2+2m-2=-(m-1)2-1<0,
所以由f(-m2-1)>f(-m2+2m-2)得,
$\left\{{\begin{array}{l}{-3≤-{m^2}-1≤0}\\{-3≤-{m^2}+2m-2≤0}\\{-{m^2}-1<-{m^2}+2m-2}\end{array}}\right.$,
解得$\frac{1}{2}<m≤\sqrt{2}$.
故选:D
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性的关系,将不等式进行转化是解决本题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2015}{2}$ | B. | 1006 | C. | 1007 | D. | 1008 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<4或x>6} | B. | {x|x<-6或x>-4} | C. | {x|4<x<6} | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{2}$ | C. | -$\frac{π}{6}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
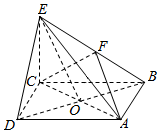 如图,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
如图,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com