
分析 设$\overline{OA}$=x$\overrightarrow{a}$,$\overrightarrow{OB}$=y$\overrightarrow{b}$,用$\overrightarrow{a},\overrightarrow{b}$表示出$\overrightarrow{PA},\overrightarrow{PB}$,得出$\overrightarrow{PA}•\overrightarrow{PB}$关于x,y的函数,利用基本不等式得出最值.
解答 解:设OA=x,OB=y,则xy=2,$\overline{OA}$=x$\overrightarrow{a}$,$\overrightarrow{OB}$=y$\overrightarrow{b}$,
∵OA⊥OB,∴$\overrightarrow{a}•\overrightarrow{b}=0$.
∵$\overrightarrow{a}$=$\frac{\overrightarrow{OA}}{|\overrightarrow{OA}|}$,$\overrightarrow{b}$=$\frac{\overrightarrow{OB}}{|\overrightarrow{OB}|}$,∴${\overrightarrow{a}}^{2}$=${\overrightarrow{b}}^{2}$=1.
∴$\overrightarrow{PA}$=$\overrightarrow{OA}-\overrightarrow{OP}$=(x-1)$\overrightarrow{a}$-2$\overrightarrow{b}$.$\overrightarrow{PB}$=$\overrightarrow{OB}-\overrightarrow{OP}$=-$\overrightarrow{a}$+(y-2)$\overrightarrow{b}$.
∴$\overrightarrow{PA}•\overrightarrow{PB}$=[(x-1)$\overrightarrow{a}$-2$\overrightarrow{b}$]•[-$\overrightarrow{a}$+(y-2)$\overrightarrow{b}$]=(1-x)${\overrightarrow{a}}^{2}$-2(y-2)${\overrightarrow{b}}^{2}$=5-(x+2y).
∵x+2y≥2$\sqrt{2xy}$=4.
∴5-(x+2y)≤1.
故答案为:1.
点评 本题考查了平面向量的数量级运算,基本不等式的应用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
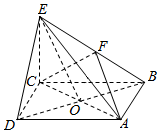 如图,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
如图,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组别 | [30,40] | [40,50] | [50,60] | [60,70] | [70,80] | [80,90] | [90,100] |
| 频数 | 3 | 10 | 12 | 15 | 6 | 2 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com