
分析 (1)根据直线y=$\frac{a}{e}$x(a≠0)为曲线y=f(x)的一条切线,求实数a的值;
(2)记F(x)=f(x)-(x-$\frac{1}{x}$),x>0.考察y=F(x)的符号,得出g(x)=$\left\{\begin{array}{l}{x-\frac{1}{x},0<x≤{x}_{0}}\\{\frac{{x}^{2}}{{e}^{x}},x>{x}_{0}}\end{array}\right.$,再分类讨论,利用导数的正负,即可得出结论.
解答 解:(1)设切点坐标为(x0,y0),f′(x)=$\frac{x(2-x)}{{e}^{x}}$,则$\left\{\begin{array}{l}{\frac{a}{e}{x}_{0}=\frac{{{x}_{0}}^{2}}{{e}^{{x}_{0}}}}\\{\frac{a}{e}=\frac{{x}_{0}(2-{x}_{0})}{{e}^{{x}_{0}}}}\end{array}\right.$,∴a=1;
(2)记F(x)=f(x)-(x-$\frac{1}{x}$),x>0.下面考察y=F(x)的符号.
求导F′(x)=$\frac{x(2-x)}{{e}^{x}}$-1-$\frac{1}{{x}^{2}}$,
x≥2,F′(x)<0,0<x<2,x(2-x)≤1,∴F′(x)=$\frac{x(2-x)}{{e}^{x}}$-1-$\frac{1}{{x}^{2}}$≤-$\frac{1}{{x}^{2}}$<0,
∴F(x)在(0,+∞)上单调递减,
∵F(1)=$\frac{1}{e}$>0,F(2)=$\frac{4}{{e}^{2}}$-$\frac{3}{2}$<0,
∴F(x)在[1,2]上有唯一零点x0,
∴g(x)=$\left\{\begin{array}{l}{x-\frac{1}{x},0<x≤{x}_{0}}\\{\frac{{x}^{2}}{{e}^{x}},x>{x}_{0}}\end{array}\right.$,
∴h(x)=g(x)-bx2=$\left\{\begin{array}{l}{x-\frac{1}{x}-b{x}^{2},0<x≤{x}_{0}}\\{\frac{{x}^{2}}{{e}^{x}}-b{x}^{2},x>{x}_{0}}\end{array}\right.$,
x>x0,h′(x)=$\frac{x(2-x)}{{e}^{x}}$-2bx≥0恒成立,∴2b≤$\frac{2-x}{{e}^{x}}$,
设u(x)=$\frac{2-x}{{e}^{x}}$,u′(x)=$\frac{x-3}{{e}^{x}}$,函数在(x0,3)上单调递减,(3,+∞)上单调递增,
∴u(x)min=-$\frac{1}{{e}^{2}}$,∴2b≤-$\frac{1}{{e}^{2}}$,∴b≤-$\frac{1}{2{e}^{2}}$;
0<x≤x0时,h′(x)=1+$\frac{1}{{x}^{2}}$-2bx,b≤0,h′(x)>0在(0,x0)上恒成立,
综上所述,b≤-$\frac{1}{2{e}^{2}}$时,函数h(x)=g(x)-bx2为增函数.
点评 本题考查导数的几何意义,考查函数的单调性,最值,考查学生分析解决问题的能力,属于中档题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,1] | C. | (-1,1) | D. | (-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q | B. | (¬p)∨q | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
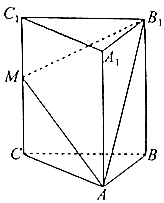 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,M是CC1中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,M是CC1中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}-\frac{3}{2}i$ | B. | $\frac{1}{2}+\frac{3}{2}i$ | C. | 1+3i | D. | 1-3i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
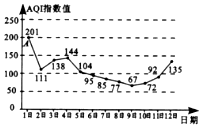 AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )
AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )| A. | 这12天中有6天空气质量为“优良” | B. | 这12天中空气质量最好的是4月9日 | ||
| C. | 这12天的AQI指数值的中位数是90 | D. | 从4日到9日,空气质量越来越好 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com