
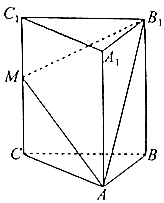
 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,M是CC1中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,M是CC1中点.分析 (1)连结A1B交AB于P,则P是A1B的中点,取AB中点D,连结CD、PD、MP,推导出四边形MCDP是平行四边形,从而CD∥MP,求出CD⊥AB,CC1⊥CD,CD⊥AA1,从而MP⊥平面A1ABB1,由此能证明平面AB1M⊥平面A1ABB1.
(2)取AB中点D,BB1中点N,连结CD、CN、DN,则截面CDN是过点C与平面AB1M平行的截面.利用面面垂直的判定定理能证明平面CDN∥平面AB1M.
解答 证明:(1)连结A1B交AB于P,则P是A1B的中点,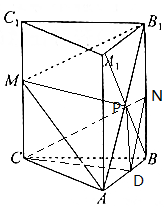 取AB中点D,连结CD、PD、MP,
取AB中点D,连结CD、PD、MP,
∵M、D分别是CC1、AB的中点,
∴DP∥CM,且DP=CM,
∴四边形MCDP是平行四边形,
∴CD∥MP,∵AC=BC,∴CD⊥AB,
∵CC1⊥平面ABC,∴CC1⊥CD,
又AA1∥CC1,∴CD⊥AA1,
∴CD⊥平面A1ABB1,∴MP⊥平面A1ABB1,
又∵MP?平面AB1M,
∴平面AB1M⊥平面A1ABB1.
解:(2)取AB中点D,BB1中点N,
连结CD、CN、DN,则截面CDN是过点C与平面AB1M平行的截面.
理由如下:
∵D、N分别是AB、BB1的中点,∴DN∥AB1,
又在矩形BCC1B1中,M是CC1的中点,
∴B1N∥CM,B1N=CM,
∴四边形CMB1N是平行四边形,∴B1M∥CN,
∵CN、DN?平面AB1M,B1M、AB1?平面AB1M,
∴CN∥平面AB1M,DN∥平面AB1M,
∵CN∩DN=N,CN、DN?平面CDN,
∴平面CDN∥平面AB1M.
点评 本题考查面面垂直、面面平行的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,数形结合思想,考查创新意识、应用意识,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{e^2}{2}$ | B. | $\frac{{3{e^2}}}{2}$ | C. | $\frac{e^2}{4}$ | D. | $\frac{e^2}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
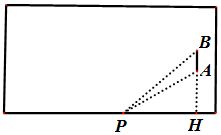 如图所示的矩形是长为100码,宽为80码的足球比赛场地.其中PH是足球场地边线所在的直线,AB是球门,且AB=8码.从理论研究及经验表明:当足球运动员带球沿着边线奔跑时,当运动员(运动员看做点P)所对AB的张角越大时,踢球进球的可能性就越大.
如图所示的矩形是长为100码,宽为80码的足球比赛场地.其中PH是足球场地边线所在的直线,AB是球门,且AB=8码.从理论研究及经验表明:当足球运动员带球沿着边线奔跑时,当运动员(运动员看做点P)所对AB的张角越大时,踢球进球的可能性就越大.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
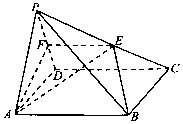 如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E在棱PC上(异于点P,C),平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E在棱PC上(异于点P,C),平面ABE与棱PD交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{23}{12}π$ | B. | $\frac{35}{12}π$ | C. | $\frac{19}{6}π$ | D. | $\frac{59}{12}π$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com