
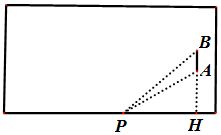
 如图所示的矩形是长为100码,宽为80码的足球比赛场地.其中PH是足球场地边线所在的直线,AB是球门,且AB=8码.从理论研究及经验表明:当足球运动员带球沿着边线奔跑时,当运动员(运动员看做点P)所对AB的张角越大时,踢球进球的可能性就越大.
如图所示的矩形是长为100码,宽为80码的足球比赛场地.其中PH是足球场地边线所在的直线,AB是球门,且AB=8码.从理论研究及经验表明:当足球运动员带球沿着边线奔跑时,当运动员(运动员看做点P)所对AB的张角越大时,踢球进球的可能性就越大.分析 (1)计算tan∠APH与tan∠BPH的值,利用两角差的正切公式求出tan∠APB的值;
(2)设PH=x,x∈(0,100),计算tan∠APH、tan∠BPH的值,求出tan∠APB的解析式,利用基本不等式求出它的最大值即可.
解答 解:(1)AB=8,AH=40-4=36,PH=20,
∴tan∠APH=$\frac{36}{20}$=$\frac{9}{5}$,
tan∠BPH=$\frac{36+8}{20}$=$\frac{11}{5}$,
∴tan∠APB=tan(∠BPH-∠APH)
=$\frac{\frac{11}{5}-\frac{9}{5}}{1+\frac{11}{5}×\frac{9}{5}}$
=$\frac{5}{62}$;
即PH=20,tan∠APB的值为$\frac{5}{62}$;
(2)设PH=x,x∈(0,100),
∴tan∠APH=$\frac{36}{x}$,tan∠BPH=$\frac{44}{x}$,
∴tan∠APB=tan(∠BPH-∠APH)
=$\frac{\frac{44}{x}-\frac{36}{x}}{1+\frac{44}{x}•\frac{36}{x}}$
=$\frac{8x}{{x}^{2}+44×36}$
=$\frac{8}{x+\frac{44×36}{x}}$≤$\frac{8}{2\sqrt{x•\frac{44×36}{x}}}$
=$\frac{4}{12\sqrt{11}}$
=$\frac{\sqrt{11}}{33}$,当且仅当x=12$\sqrt{11}$时取“=”;
∴当运动员P沿着边线带球行进时,离AB所在直线的距离为12$\sqrt{11}$码开始射门进球的可能性会最大.
点评 本题考查了三角函数的恒等变换与应用问题,是综合题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $-\frac{1}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,1] | C. | (-1,1) | D. | (-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
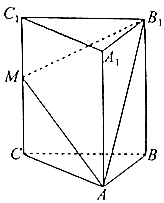 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,M是CC1中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,M是CC1中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [0,$\sqrt{2}$] | C. | [$-\sqrt{2}$,$\sqrt{2}$] | D. | [-2,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com