
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $-\frac{1}{4}$ | D. | $\frac{1}{4}$ |
分析 由已知利用倍角公式,同角三角函数基本关系式化简可求$\frac{6sinθcosθ}{si{n}^{2}θ+co{s}^{2}θ}$=4tanθ,由已知可得tanθ≠0,进而可求tan2θ=$\frac{1}{2}$,利用倍角公式,同角三角函数基本关系式可求cos2θ的值.
解答 解:∵3sin2θ=4tanθ,
∴$\frac{6sinθcosθ}{si{n}^{2}θ+co{s}^{2}θ}$=$\frac{6tanθ}{1+ta{n}^{2}θ}$=4tanθ,
∵θ≠kπ(k∈Z),tanθ≠0,
∴$\frac{3}{1+ta{n}^{2}θ}$=2,解得:tan2θ=$\frac{1}{2}$,
∴cos2θ=$\frac{1-ta{n}^{2}θ}{1+ta{n}^{2}θ}$=$\frac{1-\frac{1}{2}}{1+\frac{1}{2}}$=$\frac{1}{3}$.
故选:B.
点评 本题主要考查了倍角公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:选择题
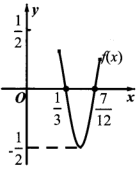 函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )
函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )| A. | $(-\frac{1}{24}+2kπ,\frac{5}{24}+2kπ)$,(k∈Z) | B. | $(-\frac{1}{12}+\frac{k}{2},\frac{5}{12}+\frac{k}{2})$,(k∈Z) | ||
| C. | $(-\frac{1}{12}+2kπ,\frac{1}{3}+2kπ)$,(k∈Z) | D. | $(-\frac{1}{24}+\frac{k}{2},\frac{5}{24}+\frac{k}{2})$,(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{e^2}{2}$ | B. | $\frac{{3{e^2}}}{2}$ | C. | $\frac{e^2}{4}$ | D. | $\frac{e^2}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -3 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
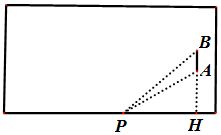 如图所示的矩形是长为100码,宽为80码的足球比赛场地.其中PH是足球场地边线所在的直线,AB是球门,且AB=8码.从理论研究及经验表明:当足球运动员带球沿着边线奔跑时,当运动员(运动员看做点P)所对AB的张角越大时,踢球进球的可能性就越大.
如图所示的矩形是长为100码,宽为80码的足球比赛场地.其中PH是足球场地边线所在的直线,AB是球门,且AB=8码.从理论研究及经验表明:当足球运动员带球沿着边线奔跑时,当运动员(运动员看做点P)所对AB的张角越大时,踢球进球的可能性就越大.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
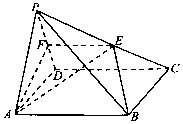 如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E在棱PC上(异于点P,C),平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E在棱PC上(异于点P,C),平面ABE与棱PD交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com