
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | -2 | C. | -1 | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2] | B. | [2+∞) | C. | (1,3] | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若a>b>0,则$\frac{1}{a}$<$\frac{1}{b}$”的逆命题是真命题 | |
| B. | 命题p:?x∈R,x2-x+1>0,则¬p:?x0∈R,x02-x0+1<0 | |
| C. | “a>1,b>1”是“ab>1”成立的充分条件 | |
| D. | “a>b”是“a2>b2”成立的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源:2017届山东潍坊临朐县高三10月月考数学(文)试卷(解析版) 题型:选择题
已知集合 ,若对于任意
,若对于任意 ,存在
,存在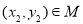 ,使得
,使得 成立,则称集合
成立,则称集合 是“理想集合”.给出下列4个集合:
是“理想集合”.给出下列4个集合:
① ;
;
② ;
;
③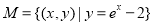 ;
;
④ .
.
其中所有“理想集合”的序号是( )
A.①③ B.②③
C.②④ D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com