
| A. | (1,2] | B. | [2+∞) | C. | (1,3] | D. | [3,+∞) |
分析 化简$\frac{|P{F}_{1}{|}^{2}}{|P{F}_{2}|}$=$\frac{(2a+|P{F}_{2}|)^{2}}{|P{F}_{2}|}$=$\frac{4{a}^{2}}{|P{F}_{2}|}$+4a+|PF2|,利用基本不等式,再利用焦半径公式,即可求出双曲线离心率的取值范围.
解答 解:由定义知:|PF1|-|PF2|=2a,所以|PF1|=2a+|PF2|,
所以$\frac{|P{F}_{1}{|}^{2}}{|P{F}_{2}|}$=$\frac{(2a+|P{F}_{2}|)^{2}}{|P{F}_{2}|}$=$\frac{4{a}^{2}}{|P{F}_{2}|}$+4a+|PF2|≥8a,
当且仅当$\frac{4{a}^{2}}{|P{F}_{2}|}$=|PF2|,即|PF2|=2a时取得等号
设P(x0,y0) (x0≤-a)
由焦半径公式得:|PF2|=-ex0-a=2a
所以ex0=-3a
所以e=-$\frac{3a}{{x}_{0}}$≤3
又双曲线的离心率e>1
所以e∈(1,3]
故选:C.
点评 本题考查双曲线离心率的取值范围,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生 | 1号 | 2号 | 3号 | 4号 | 5号 |
| 甲班 | 6 | 5 | 7 | 9 | 8 |
| 乙班 | 4 | 8 | 9 | 7 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(理)试卷(解析版) 题型:解答题
四棱锥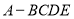 中,底面
中,底面 为矩形,侧面
为矩形,侧面 底面
底面 ,
, ,
, ,
, .
.

(1)证明: ;
;
(2)设 与平面
与平面 所成的角为
所成的角为 ,求二面角
,求二面角 的余弦值的大小.
的余弦值的大小.
查看答案和解析>>
科目:高中数学 来源:2017届江西省红色七校高三上学期联考一数学(文)试卷(解析版) 题型:解答题
已知函数 ,当
,当 时,函数
时,函数 的图象关于
的图象关于 轴对称,数列
轴对称,数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com