
分析 (1)本题是一个古典概型,用(a,b)表示一枚骰子投掷两次所得到的点数的事件,基本事件(a,b)的总数有36个满足条件的事件是二次方程x2-2(a-2)x-b2+12=0有两正根,根据实根分布得到关系式,得到概率.
(2)本题是一个几何概型,试验的全部结果构成区域Ω={(a,b)|2≤a≤6,0≤b≤4},满足条件的事件为:B={(a,b)|2≤a≤6,0≤b≤4,(a-2)2+b2≥12},做出两者的面积,得到概率.
解答 解:(1)记“方程有两个正根”为事件A,基本事件(a,b)共有36个…(2分)
方程有正根等价于$\left\{\begin{array}{l}{a-2>0}\\{12-{b}^{2}>0}\\{(a-2)^{2}+{b}^{2}≥12}\end{array}\right.$,
则事件A包含的基本事件为(4,3)、(5,2)、(5,3)、(6,1)、(6,2)、(6,3)共6个…(4分)
P(A)=$\frac{6}{36}$=$\frac{1}{6}$…(6分)
故所求的概率为$\frac{1}{6}$…(7分)
(2)记“方程无实根”为事件B,试验的全部结果构成区域Ω={(a,b)|2≤a≤6,0≤b≤4},
其面积为S(Ω)=16
满足条件的事件为:B={(a,b)|2≤a≤6,0≤b≤4,(a-2)2+b2≥12},
其面积为S(B)=16-3π…(11分)
P(B)=1-$\frac{3π}{16}$…(13分)
故所求的概率为1-$\frac{3π}{16}$…(14分)
点评 本题考查古典概型和几何概型,几何概型和古典概型是高中必修中学习的,高考时常以选择和填空出现,有时文科会考这种类型的解答题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校高三文,理各两个班在11月份进行了一次质量考试,考生成绩情况如下表所示:已知用分层抽样方法在分数[400,480)的考生中随机抽取27名考生进行质量分析,其中文科考生抽取了7名.(1)求a的值(2)如图是文科不低于550分的5名考生的语文成绩(其中语文满分为150分)的茎叶图,请计算这5名考生的语文成绩的方差;(3)在成绩不低于550分的所有考生中抽取2名进行治疗分析,求至少抽到一名理科生的概率.
某校高三文,理各两个班在11月份进行了一次质量考试,考生成绩情况如下表所示:已知用分层抽样方法在分数[400,480)的考生中随机抽取27名考生进行质量分析,其中文科考生抽取了7名.(1)求a的值(2)如图是文科不低于550分的5名考生的语文成绩(其中语文满分为150分)的茎叶图,请计算这5名考生的语文成绩的方差;(3)在成绩不低于550分的所有考生中抽取2名进行治疗分析,求至少抽到一名理科生的概率. | [0,400] | [400,480] | [480,550] | [550,750] | |
| 文科考生 | 67 | 35 | 19 | 5 |
| 理科考生 | 53 | a | 41 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
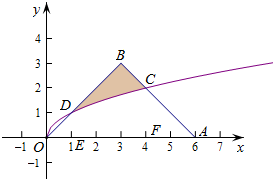 如图,等腰三角形OAB的顶点A、B的坐标分别为(6,0),(3,3),且AB与曲线y=$\sqrt{x}$交于点C,在△OAB中任取一点P,则点P落在阴影部分的概率为( )
如图,等腰三角形OAB的顶点A、B的坐标分别为(6,0),(3,3),且AB与曲线y=$\sqrt{x}$交于点C,在△OAB中任取一点P,则点P落在阴影部分的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{27}$ | D. | $\frac{11}{54}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com