
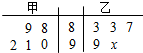
 下面茎叶图表示的甲、乙两人在5次综合测评中的成绩,其中一个数字x被污损,则甲的平均成绩超过乙的平均成绩的概率是( )
下面茎叶图表示的甲、乙两人在5次综合测评中的成绩,其中一个数字x被污损,则甲的平均成绩超过乙的平均成绩的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{4}{5}$ | D. | $\frac{9}{10}$ |
分析 由已知的茎叶图,我们可以求出甲乙两人的平均成绩,然后求出$\overline{甲}$≤$\overline{乙}$,
即甲的平均成绩不超过乙的平均成绩的概率,进而根据对立事件求出答案.
解答 解:由茎叶图中的数据得,
甲的5次综合测评中的成绩分别为88,89,90,91,92,
则甲的平均成绩$\overline{甲}$=$\frac{1}{5}$(88+89+90+91+92)=90;
设污损数字为x,
则乙的5次综合测评中的成绩分别为83,83,87,99,90+x,
则乙的平均成绩$\overline{乙}$=$\frac{1}{5}$[83+83+87+99+(90+x)]=88.4+$\frac{x}{5}$,
当x=8或9时,$\overline{甲}$≤$\overline{乙}$,
即甲的平均成绩不超过乙的平均成绩的概率为$\frac{2}{10}$=$\frac{1}{5}$;
则甲的平均成绩超过乙的平均成绩的概率P=1-$\frac{1}{5}$=$\frac{4}{5}$.
故选:C.
点评 本题考查了平均数、茎叶图与古典概型的概率计算公式问题,根据茎叶图求出数据的平均数是解题的关键.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,0] | B. | (0,1) | C. | (2,3] | D. | (-2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.50 | B. | 0.40 | C. | 0.43 | D. | 0.48 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在α,β∈R,使tan(α+β)=tan α+tan β | |
| B. | 对任意x>0,有lg2x+lg x+1>0 | |
| C. | △ABC中,A>B的充要条件是sin A>sin B | |
| D. | 对任意φ∈R,函数y=sin(2x+φ)都不是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com