
分析 (1)由${a}_{n}=\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$,能求出an.
(2)由${b_n}=\frac{1}{S_n}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,利用裂项求和法能求出数列{bn}的前n项和Tn.
解答 解:(1)∵数列{an}的前n(n∈N+)项和${S_n}={n^2}+2n$.
∴a1=S1=3…(1分)
n≥2时,${a_n}={S_n}-{S_{n-1}}=({n^2}+2n)-[{(n-1)^2}+2(n-1)]=2n+1$…(5分)
a1=3满足an=2n+1,
∴?n∈N+,an=2n+1…(6分)
(2)∵${b_n}=\frac{1}{S_n}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$…(7分),
∴n≥3时,${b_1}+{b_2}+…+{b_n}=\frac{1}{2}[(\frac{1}{1}-\frac{1}{3})+(\frac{1}{2}-\frac{1}{4})+(\frac{1}{3}-\frac{1}{5})+…+(\frac{1}{n}-\frac{1}{n+2})]$…(9分)
=$\frac{1}{2}(\frac{1}{1}+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$…(10分)
=$\frac{{3{n^2}+5n}}{4(n+1)(n+2)}$…(11分),
检验知,n=1,n=2时,${T_n}=\frac{{3{n^2}+5n}}{4(n+1)(n+2)}$也成立,
所以,?n∈N+,${T_n}=\frac{{3{n^2}+5n}}{4(n+1)(n+2)}$.…(12分)
点评 本题考查数列的通项公式、前n项和的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ③④ | C. | ①② | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
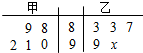 下面茎叶图表示的甲、乙两人在5次综合测评中的成绩,其中一个数字x被污损,则甲的平均成绩超过乙的平均成绩的概率是( )
下面茎叶图表示的甲、乙两人在5次综合测评中的成绩,其中一个数字x被污损,则甲的平均成绩超过乙的平均成绩的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{4}{5}$ | D. | $\frac{9}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为45°,则此山的高度CD=300$\sqrt{2}$m.
如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为45°,则此山的高度CD=300$\sqrt{2}$m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com