
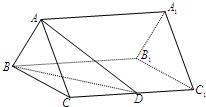
 如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧BB1C1C所成的角为45°.
如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧BB1C1C所成的角为45°.分析 (1)取BC中点E,连AE.推导出AE⊥BC.AE⊥侧面BB1C1C.连ED,则直线AD与侧面BB1C1C所成的角为∠ADE=45°.由此能求出正三棱柱的侧棱长.
(2)过E作EF⊥BD于F,连AF,则∠AFE为二面角A-BD-C的平面角,由此能求出二面角A-BD-C的平面角的正切.
(3)由BD⊥平面AEF,知平面AEF⊥平面ABD,且交线为AF,过E作EG⊥AF于G,则EG⊥平面ABD,由此能求出点C到平面ABD的距离.
解答 解:(1)设正三棱柱ABC-A1B1C1的侧棱长为x.取BC中点E,连AE.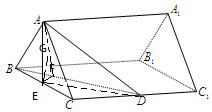
∵△ABC是正三角形,∴AE⊥BC.
又底面ABC⊥侧面BB1C1C,且交线为BC.
∴AE⊥侧面BB1C1C.
连ED,则直线AD与侧面BB1C1C所成的角为∠ADE=45°.
在Rt△AED中,tan45°=$\frac{AE}{ED}$=$\frac{\sqrt{3}}{\sqrt{1+\frac{{x}^{2}}{4}}}$,解得x=2$\sqrt{2}$.
∴此正三棱柱的侧棱长为2$\sqrt{2}$. …(4分)
(2)过E作EF⊥BD于F,连AF,
∵AE⊥侧面BB1C1C,∴AF⊥BD.
∴∠AFE为二面角A-BD-C的平面角.
在Rt△BEF中,EF=BEsin∠EBF,
又BE=1,sin$∠EBF=\frac{CD}{BD}$=$\frac{\sqrt{2}}{\sqrt{{2}^{2}+(\sqrt{2})^{2}}}$=$\frac{\sqrt{3}}{3}$,∴EF=$\frac{\sqrt{3}}{3}$.
又AE=$\sqrt{3}$,∴在Rt△AEF中,tan$∠AFE=\frac{AE}{EF}$=3.
故二面角A-BD-C的平面角的正切为3. …(9分)
(3)由(2)知,BD⊥平面AEF,
∴平面AEF⊥平面ABD,且交线为AF,
∴过E作EG⊥AF于G,则EG⊥平面ABD.
在Rt△AEF中,EG=$\frac{AE×EF}{AF}$=$\frac{\sqrt{3}×\frac{\sqrt{3}}{3}}{\sqrt{(\sqrt{3})^{2}+(\frac{\sqrt{3}}{3})^{2}}}$=$\frac{\sqrt{30}}{10}$.
∵E为BC中点,∴点C到平面ABD的距离为2EG=$\frac{2\sqrt{30}}{10}$=$\frac{\sqrt{30}}{5}$. …(14分)
点评 本题考查正三棱柱的侧棱长、二面角的正切值、点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{6}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | p |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:(1)SG⊥平面EFG;(2)SD⊥平面EFG;(3)GF⊥平面SEF;(4)EF⊥平面GSD;(5)GD⊥平面SEF.正确的是( )
如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:(1)SG⊥平面EFG;(2)SD⊥平面EFG;(3)GF⊥平面SEF;(4)EF⊥平面GSD;(5)GD⊥平面SEF.正确的是( )| A. | (1)和(3) | B. | (2)和(5) | C. | (1)和(4) | D. | (2)和(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
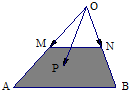 如图所示,在△OAB中,M、N分别是OA、OB的中点,点P在梯形ABNM区域(含边界)上移动,且$\overrightarrow{OP}=x\overrightarrow{OM}+y\overrightarrow{ON}$,则4x+3y的取值范围是[3,8].
如图所示,在△OAB中,M、N分别是OA、OB的中点,点P在梯形ABNM区域(含边界)上移动,且$\overrightarrow{OP}=x\overrightarrow{OM}+y\overrightarrow{ON}$,则4x+3y的取值范围是[3,8].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com