
分析 (Ⅰ)根据分母不为0,对数函数定义求出f(x)的定义域,进而求出a=e的f(x)解析式,求出导函数,根据导函数的正负确定出函数的单调区间,即可求出f(x)的极小值;
(Ⅱ)把导函数代入g(x)=f′(x)-$\frac{x}{3}$,表示出g(x),令g(x)=0,表示出a,利用导函数的性质确定出g(x)零点个数即可;
(Ⅲ)对任意的m>n>0,$\frac{f(m)-f(n)}{m-n}$<1恒成立,等价于f(m)-m<f(n)-n恒成立(*),设h(x)=f(x)-x=lnx+$\frac{a}{x}$-x(x>0),故(*)等价于h(x)在(0,+∞)上单调递减,进而求出a的最小值,确定出a的范围即可.
解答 解:(Ⅰ)f(x)的定义域为(0,+∞),
当a=e时,f(x)=lnx+$\frac{e}{x}$,则f′(x)=$\frac{x-e}{{x}^{2}}$,
∴当x∈(0,e)时,f′(x)<0,f(x)在(0,e)上单调递减;
当x∈(e,+∞)时,f′(x)>0,f(x)在(e,+∞)上单调递增,
∴x=e时,f(x)取得极小值f(e)=lne+$\frac{e}{e}$=2,
∴f(x)的极小值为2;
(Ⅱ)由题设g(x)=f′(x)-$\frac{x}{3}$=$\frac{1}{x}$-$\frac{a}{x^2}$-$\frac{x}{3}$(x>0),
令g(x)=0,得a=-$\frac{1}{3}$x3+x(x>0),
设φ(x)=-$\frac{1}{3}$x3+x(x≥0),则φ′(x)=-x2+1=-(x-1)(x+1),
当x∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上单调递增;
当x∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上单调递减,
∴x=1是φ(x)的唯一极值点,且是极大值点,
∴x=1也是φ(x)的最大值点,
∴φ(x)的最大值为φ(1)=$\frac{2}{3}$.
又φ(0)=0,结合y=φ(x)的图象(如图所示),可知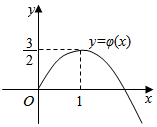
①当a>$\frac{2}{3}$时,函数g(x)无零点;
②当a=$\frac{2}{3}$时,函数g(x)有且只有一个零点;
③当0<a<$\frac{2}{3}$时,函数g(x)有两个零点;
④当a≤0时,函数g(x)有且只有一个零点(x>0),
综上所述,当a>$\frac{2}{3}$时,函数g(x)无零点;
当a=$\frac{2}{3}$或a≤0时,函数g(x)有且只有一个零点;
当0<a<$\frac{2}{3}$时,函数g(x)有两个零点;
(Ⅲ)对任意的m>n>0,$\frac{f(m)-f(n)}{m-n}$<1恒成立,
等价于f(m)-m<f(n)-n恒成立(*),
设h(x)=f(x)-x=lnx+$\frac{a}{x}$-x(x>0),
∴(*)等价于h(x)在(0,+∞)上单调递减,
由h′(x)=$\frac{1}{x}$-$\frac{a}{x^2}$-1≤0在(0,+∞)上恒成立,
得a≥-x2+x=-(x-$\frac{1}{2}$)2+$\frac{1}{4}$(x>0)恒成立,
∴a≥$\frac{1}{4}$(对a=$\frac{1}{4}$,h′(x)=0仅在x=$\frac{1}{2}$时成立),
∴a的取值范围是[$\frac{1}{4}$,+∞).
点评 此题考查了利用导数研究函数的单调性,利用导数求函数的极值,以及利用导数求函数在闭区间上的最值,熟练掌握导数的性质是解本题的关键.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 课程 人数 班级 | 选修4-1 | 选修4-4 | 选修4-5 |
| A | 10 | a | 15 |
| B | 10 | 20 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某校为了对初三学生的体重进行摸底调查,随机抽取了50名学生的体重(kg),将所得数据整理后,画出了频率分布直方图,体重在[45,50)内适合跑步训练,体重在[50,55)内适合跳远训练,体重在[55,60)内适合投掷相关方面训练,试估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为( )
某校为了对初三学生的体重进行摸底调查,随机抽取了50名学生的体重(kg),将所得数据整理后,画出了频率分布直方图,体重在[45,50)内适合跑步训练,体重在[50,55)内适合跳远训练,体重在[55,60)内适合投掷相关方面训练,试估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为( )| A. | 4:3:1 | B. | 5:3:1 | C. | 5:3:2 | D. | 3:2:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |z|=2 | B. | $\overline{z}$=1-i | C. | z的实部为1 | D. | z+1为纯虚数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某班m名学生在一次考试中数学成绩的频率分布直方图如图,若在这m名学生中,数学成绩不低于100分的人数为33,则m等于( )
某班m名学生在一次考试中数学成绩的频率分布直方图如图,若在这m名学生中,数学成绩不低于100分的人数为33,则m等于( )| A. | 45 | B. | 48 | C. | 50 | D. | 55 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
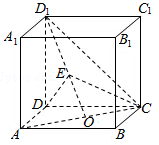 已知正方体ABCD-A1B1C1D1的棱长为2,O是AC的中点,E是线段D1O上一点,且$\overrightarrow{{D_1}E}=λ\overrightarrow{EO}$.
已知正方体ABCD-A1B1C1D1的棱长为2,O是AC的中点,E是线段D1O上一点,且$\overrightarrow{{D_1}E}=λ\overrightarrow{EO}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com